(本小題滿分14分)
已知棱長為1的正方體ABCD-A
1B
1C
1D
1中,P在對角線A
1C
1上,記二面角P-AB-C為α,二面角P-BC-A為β。
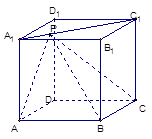
(1)當A
1P:PC
1=1:3時,求cos(α+β)的大小。
(2)點P是線段A
1C
1(包括端點)上的一個動點,問:當點P在什么位置時,α+β有最小值?
(1)-
(2)P為A
1C
1的中點
試題分析:
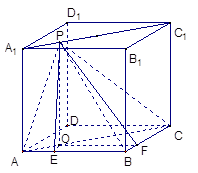
作PO⊥面ABCD于O,作OE⊥AB于E,OF⊥BC于F
∵正方體ABCD-A
1B
1C
1D
1∴點O在線段AC上,且AO:OC=1:3
∴α=∠PEO,β=∠PFO
EO=
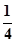
,F(xiàn)O=
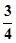
,PO=1,PE=
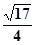
,PF=
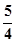
2分
cosα=
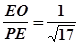
,sinα=
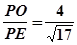
,cosβ=
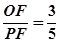
, sinβ=
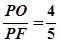
cos(α+β)=cosαcosβ-sinαsinβ=
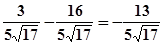
=-
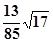
4分
(2)(8分)
設A
1P=kA
1C
1,k∈[0,1] 5分
由第(1)題可知α=∠PEO,β=∠PFO
EO=k,FO=1-k,PO=1,PE=
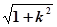
,PF=
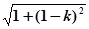
cosα=
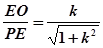
,sinα=
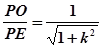
,cosβ=
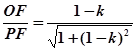
,
sinβ=
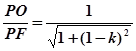
7分
當k=0或1時,即點P與A
1或C
1重合時,其中一個角為
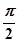
,另一個角為
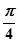
,
此時α+β=
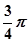
,tan(α+β)= -1 8分
∴當k≠0,且k≠1時,tanα=
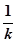
,tanβ=
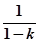
∴tan(α+β)
=
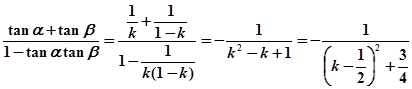
11分
∵k∈(0,1) ∴
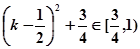
∴tan(α+β)∈
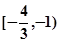
∵
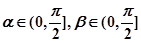
∴
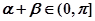
∴tan(α+β)=
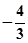
時,α+β有最小值,此時k=
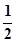
時,即點P為A
1C
1的中點。 14分
點評:本題有一定難度,多章節(jié)知識的綜合
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分14分)
如圖,四棱錐P—ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD為直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,點E在棱PA上,且PE=2EA。
(1)求直線PC與平面PAD所成角的余弦值;(6分)
(2)求證:PC//平面EBD;(4分)
(3)求二面角A—BE—D的余弦值.(4分)

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若兩條直線都與一個平面平行,則這兩條直線的位置關系是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設
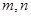
是不同的直線,
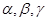
是不同的平面,有以下四個命題:
①
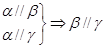
②
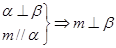
③
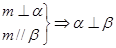
④
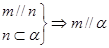
其中正確的個數(shù)( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知直線
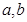
和平面
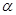
,且
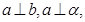
則
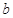
與
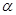
的位置關系是
.(用符號表示)
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若m、n為兩條不同的直線,α、β為兩個不同的平面,則以下命題正確的是( ).
| A.若m∥α,n∥α,則m∥n | B.若m∥n,m⊥α,則n⊥α |
| C.若m∥β,α∥β,則m∥α | D.若α∩β=m,m⊥n,則n⊥α |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
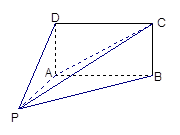
如圖,四棱錐
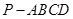
的底面
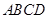
為矩形,且
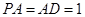
,
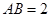
,
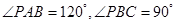
,(Ⅰ)平面
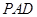
與平面
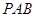
是否垂直?并說明理由;(Ⅱ)求直線
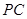
與平面
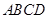
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設

是兩條不同的直線,

是三個不同的平面,給出下列四個命題:
①若

,
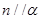
,則
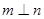
②若

,
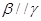
,

,則

③若

,
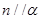
,則
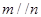
④若

,

,則

其中正確命題的序號是 _______
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
正方體
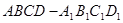
中,二面角
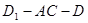
的正切值為
查看答案和解析>>


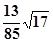 (2)P為A1C1的中點
(2)P為A1C1的中點
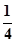 ,F(xiàn)O=
,F(xiàn)O=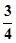 ,PO=1,PE=
,PO=1,PE=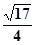 ,PF=
,PF=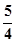 2分
2分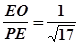 ,sinα=
,sinα=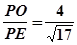 ,cosβ=
,cosβ=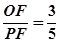 , sinβ=
, sinβ=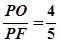
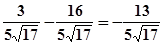 =-
=-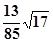 4分
4分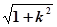 ,PF=
,PF=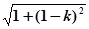
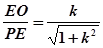 ,sinα=
,sinα=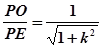 ,cosβ=
,cosβ=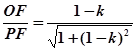 ,
, 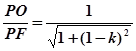 7分
7分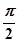 ,另一個角為
,另一個角為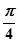 ,
,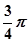 ,tan(α+β)= -1 8分
,tan(α+β)= -1 8分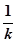 ,tanβ=
,tanβ=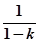
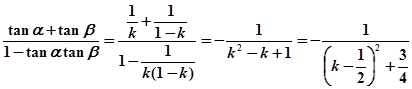 11分
11分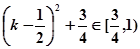 ∴tan(α+β)∈
∴tan(α+β)∈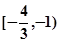
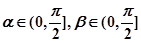 ∴
∴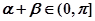
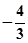 時,α+β有最小值,此時k=
時,α+β有最小值,此時k=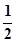 時,即點P為A1C1的中點。 14分
時,即點P為A1C1的中點。 14分

 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案
 是兩條不同的直線,
是兩條不同的直線, 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題: ,
,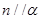 ,則
,則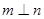 ②若
②若 ,
,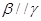 ,
, ,則
,則
 ,
,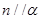 ,則
,則 ④若
④若 ,
, ,則
,則