
【題目】已知函數![]() ,其中
,其中![]() .
.
(1)若![]() 和
和![]() 在區間
在區間![]() 上具有時間的單調性,求實數
上具有時間的單調性,求實數![]() 的取值范圍;
的取值范圍;
(2)若![]() ,且函數
,且函數![]() 的最小值為
的最小值為![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
試題分析:(1)因為![]() ,
,![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上單調遞減,所以
上單調遞減,所以![]() ,且
,且![]() 單調遞增,比較
單調遞增,比較![]() 與端點
與端點![]() 的大小關系,
的大小關系,![]() 即
即![]() 時,
時,![]() ,不合題意;
,不合題意;![]() 即
即![]() 時,
時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,又
上單調遞增,又![]() 在
在![]() 上單調遞減,所以
上單調遞減,所以![]() 解得
解得![]() ;(2)
;(2)![]() ,令
,令![]() ,通過參變分離構造新函數,可判斷出在
,通過參變分離構造新函數,可判斷出在![]() 時,
時,![]() ,所以
,所以![]() 的單調性與
的單調性與![]() 的正負有關,因此
的正負有關,因此![]() 在
在![]() 單減,
單減,![]() 單增,所以
單增,所以![]() ,通過求導可求得最小值.
,通過求導可求得最小值.
試題解析:解:(1)![]() ,
,
∵![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上單調遞減,
上單調遞減,
當![]() 時,
時,![]() ,即
,即![]() 在
在![]() 上單調遞增,不合題意
上單調遞增,不合題意
當![]() 時,由
時,由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]() 的單調減區間為
的單調減區間為![]() ,單調增區間為
,單調增區間為![]()
∵![]() 和
和![]() 在區間
在區間![]() 上具有相同的單調性,
上具有相同的單調性,
∴![]() ,解得
,解得![]() ,
,
綜上,![]() 的取值范圍是
的取值范圍是![]()
(2)![]() ,
,
由![]() 得到
得到![]() ,設
,設![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
從而![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,∴
上遞增,∴![]()
當![]() 時,
時,![]() ,即
,即![]() ,
,
在![]() 上,
上,![]() 遞減;
遞減;
在![]() 上,
上,![]() 遞增,∴
遞增,∴![]() ,
,
設![]() ,
,
![]() 在
在![]() 上遞減,∴
上遞減,∴![]() ,
,
∴![]() 的最小值為0.
的最小值為0.


科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
,![]() ,
,![]() ).
).
(1)若![]() 的部分圖像如圖所示,求
的部分圖像如圖所示,求![]() 的解析式;
的解析式;
(2)在(1)的條件下,求最小正實數![]() ,使得函數
,使得函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位后所對應的函數是偶函數;
個單位后所對應的函數是偶函數;
(3)若![]() 在
在![]() 上是單調遞增函數,求
上是單調遞增函數,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某棋類游戲的規則如下:棋子的初始位置在起點處,玩家每擲出一枚骰子,朝上一面的點數即為向終點方向前進的格子數,(比如玩家一開始擲出的骰子點數為3,則走到炸彈所在位置),若踩到炸彈則返回起點重新開始,若達到終點則游戲結束.現在已知小明擲完三次骰子后游戲恰好結束,則所有不同的情況種數為__________.
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于無窮數列![]() 和函數
和函數![]() ,若
,若![]() ,則稱
,則稱![]() 是數列
是數列![]() 的母函數.
的母函數.
(Ⅰ)定義在![]() 上的函數
上的函數![]() 滿足:對任意
滿足:對任意![]() ,都有
,都有![]() ,且
,且![]() ;又數列
;又數列![]() 滿足
滿足![]() .
.
(1)求證: ![]() 是數列
是數列![]() 的母函數;
的母函數;
(2)求數列![]() 的前項
的前項![]() 和
和![]() .
.
(Ⅱ)已知![]() 是數列
是數列![]() 的母函數,且
的母函數,且![]() .若數列
.若數列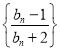 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,函數
,函數![]() .
.
(1)求證:曲線![]() 在點
在點![]() 處的切線過定點;
處的切線過定點;
(2)若![]() 是
是![]() 在區間
在區間![]() 上的極大值,但不是最大值,求實數
上的極大值,但不是最大值,求實數![]() 的取值范圍;
的取值范圍;
(3)求證:對任意給定的正數![]() ,總存在
,總存在![]() ,使得
,使得![]() 在
在![]() 上為單調函數.
上為單調函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校大一新生中的6名同學打算參加學校組織的“雅荷文學社”、“青春風街舞社”、“羽乒協會”、“演講團”、“吉他協會”五個社團,若每名同學必須參加且只能參加1個社團且每個社團至多兩人參加,則這6個人中至多有1人參加“演講團”的不同參加方法數為( )
A. 4680 B. 4770 C. 5040 D. 5200
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠2萬元設計了某款式的服裝,根據經驗,每生產1百套該款式服裝的成本為1萬元,每生產![]() (百套)的銷售額(單位:萬元)
(百套)的銷售額(單位:萬元)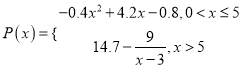 .
.
(1)若生產6百套此款服裝,求該廠獲得的利潤;
(2)該廠至少生產多少套此款式服裝才可以不虧本?
(3)試確定該廠生產多少套此款式服裝可使利潤最大,并求最大利潤.(注:利潤=銷售額-成本,其中成本=設計費+生產成本)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com