
【題目】已知函數![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)是否存在實數![]() ,使得函數
,使得函數![]() 的極值大于
的極值大于![]() ?若存在,求
?若存在,求![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
【答案】(1)當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間
,單調遞減區間
為![]() ;當
;當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,無單調遞減區間. (2)存在,范圍為
,無單調遞減區間. (2)存在,范圍為![]()
【解析】
試題(1)函數![]() 的定義域為
的定義域為![]() ,
,![]() .
.
① 當![]() 時,
時,![]() ,∵
,∵![]() ∴
∴![]() ,∴ 函數
,∴ 函數![]() 單調遞增區間為
單調遞增區間為![]()
② 當![]() 時,令
時,令![]() 得
得![]() ,即
,即![]() ,
,![]() .
.
(ⅰ)當![]() ,即
,即![]() 時,得
時,得![]() ,故
,故![]() ,
,
∴ 函數![]() 的單調遞增區間為
的單調遞增區間為![]() .
.
(ⅱ)當![]() ,即
,即![]() 時,方程
時,方程![]() 的兩個實根分別為
的兩個實根分別為![]() ,
,![]() .
.
若![]() ,則
,則![]() ,此時,當
,此時,當![]() 時,
時,![]() .
.
∴函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,若
,若![]() ,則
,則![]() ,此時,當
,此時,當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]()
∴函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() .
.
綜上所述,當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間
,單調遞減區間
為![]() ;當
;當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,無單調遞減區間.
,無單調遞減區間.
(2)由(1)得當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,故函數
上單調遞增,故函數![]() 無極值
無極值
當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ,
,
∴![]() 有極大值,其值為
有極大值,其值為![]() ,其中
,其中![]() .
.
∵![]() ,即
,即![]() , ∴
, ∴![]() .
.
設函數![]() ,則
,則![]() ,
,
∴![]() 在
在![]() 上為增函數,又
上為增函數,又![]() ,則
,則![]()
![]()
![]() ,
,
∴![]()
![]()
![]()
![]()
![]() .
.
即![]() ,結合
,結合![]() 解得
解得![]() ,∴實數
,∴實數![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】春節期間,由于高速公路繼續實行小型車免費,因此高速公路上車輛較多,某調查公司在某城市從七座以下小型汽車中按進入服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如圖的頻率分布直方圖.
(Ⅰ)此調查公司在采樣中,用到的是什么抽樣方法?
(Ⅱ)求這40輛小型車輛車速的眾數、中位數以及平均數的估計值;
(Ⅲ)若從車速在[60,70)的車輛中任抽取2輛,求至少有一輛車的車速在[65,70)的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市交通部門為了對該城市共享單車加強監管,隨機選取了100人就該城市共享單車的推行情況進行問卷調查,并將問卷中的這100人根據其滿意度評分值(百分制)按照![]() 分成5組,制成如圖所示頻率分直方圖.
分成5組,制成如圖所示頻率分直方圖.

(1)求圖中x的值;
(2)求這組數據的平均數和中位數;
(3)已知滿意度評分值在![]() 內的男生數與女生數3:2,若在滿意度評分值為
內的男生數與女生數3:2,若在滿意度評分值為![]() 的人中隨機抽取2人進行座談,求2人均為男生的概率.
的人中隨機抽取2人進行座談,求2人均為男生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某校高中男生中隨機選取100名學生,將他們的體重(單位: ![]() )數據繪制成頻率分布直方圖,如圖所示.
)數據繪制成頻率分布直方圖,如圖所示.

(1)估計該校的100名同學的平均體重(同一組數據以該組區間的中點值作代表);
(2)若要從體重在![]() ,
, ![]() 內的兩組男生中,用分層抽樣的方法選取5人,再從這5人中隨機抽取3人,記體重在
內的兩組男生中,用分層抽樣的方法選取5人,再從這5人中隨機抽取3人,記體重在![]() 內的人數為
內的人數為![]() ,求其分布列和數學期望
,求其分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面內兩點M(4,﹣2),N(2,4).
(1)求MN的垂直平分線方程;
(2)直線l經過點A(3,0),且點M和點N到直線l的距離相等,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C經過點![]() ,
,![]() 兩點,且圓心C在直線
兩點,且圓心C在直線![]() 上.
上.
(1)求圓C的方程;
(2)設![]() ,對圓C上任意一點P,在直線MC上是否存在與點M不重合的點N,使
,對圓C上任意一點P,在直線MC上是否存在與點M不重合的點N,使![]() 是常數,若存在,求出點N坐標;若不存在,說明理由.
是常數,若存在,求出點N坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是y=f(x)導函數的圖象,對于下列四個判斷:
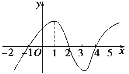
①f(x)在[-2,-1]上是增函數;
②x=-1是f(x)的極小值點;
③f(x)在[-1,2]上是增函數,在[2,4]上是減函數;
④x=3是f(x)的極小值點.
其中判斷正確的是_______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com