
【題目】已知圓C經過點![]() ,
,![]() 兩點,且圓心C在直線
兩點,且圓心C在直線![]() 上.
上.
(1)求圓C的方程;
(2)設![]() ,對圓C上任意一點P,在直線MC上是否存在與點M不重合的點N,使
,對圓C上任意一點P,在直線MC上是否存在與點M不重合的點N,使![]() 是常數,若存在,求出點N坐標;若不存在,說明理由.
是常數,若存在,求出點N坐標;若不存在,說明理由.
 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】十九大以來,國家深入推進精準脫貧,加大資金投入,強化社會幫扶,為了更好的服務于人民,派調查組到某農村去考察和指導工作.該地區有200戶農民,且都從事水果種植,據了解,平均每戶的年收入為3萬元.為了調整產業結構,調查組和當地政府決定動員部分農民從事水果加工,據估計,若能動員![]() 戶農民從事水果加工,則剩下的繼續從事水果種植的農民平均每戶的年收入有望提高
戶農民從事水果加工,則剩下的繼續從事水果種植的農民平均每戶的年收入有望提高![]() ,而從事水果加工的農民平均每戶收入將為
,而從事水果加工的農民平均每戶收入將為![]() 萬元.
萬元.
(1)若動員![]() 戶農民從事水果加工后,要使從事水果種植的農民的總年收入不低于動員前從事水果種植的農民的總年收入,求
戶農民從事水果加工后,要使從事水果種植的農民的總年收入不低于動員前從事水果種植的農民的總年收入,求![]() 的取值范圍;
的取值范圍;
(2)在(1)的條件下,要使這200戶農民中從事水果加工的農民的總收入始終不高于從事水果種植的農民的總收入,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 的圖象經過點
的圖象經過點![]() ,且相鄰的兩條對稱軸之間的距離為
,且相鄰的兩條對稱軸之間的距離為![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)若將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位后得到函數
個單位后得到函數![]() 的圖象,當
的圖象,當![]() 時,
時,![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是拋物線
是拋物線![]() 上的一點,過點
上的一點,過點![]() 作兩條直線
作兩條直線![]() 與
與![]() ,分別與拋物線相交于異于點
,分別與拋物線相交于異于點![]() 的
的![]() 兩點.
兩點.
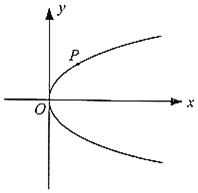
![]() 若直線
若直線![]() 過點
過點![]() 且
且![]() 的重心
的重心![]() 在
在![]() 軸上,求直線
軸上,求直線![]() 的斜率;
的斜率;
![]() 若直線
若直線![]() 的斜率為1且
的斜率為1且![]() 的垂心
的垂心![]() 在
在![]() 軸上,求直線
軸上,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北方某市一次全市高中女生身高統計調查數據顯示:全市![]() 名高中女生的身高(單位:
名高中女生的身高(單位: ![]() )服從正態分布
)服從正態分布![]() .現從某高中女生中隨機抽取
.現從某高中女生中隨機抽取![]() 名測量身高,測量發現被測學生身高全部在
名測量身高,測量發現被測學生身高全部在![]() 和
和![]() 之間,現將測量結果按如下方式分成
之間,現將測量結果按如下方式分成![]() 組:第
組:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,…,第
,…,第![]() 組
組![]() ,下圖是按上述分組方法得到的頻率分布直方圖.
,下圖是按上述分組方法得到的頻率分布直方圖.

(1)求這![]() 名女生身高不低于
名女生身高不低于![]() 的人數;
的人數;
(2)在這![]() 名女生身高不低于
名女生身高不低于![]() 的人中任意抽取
的人中任意抽取![]() 人,將該
人,將該![]() 人中身高排名(從高到低)在全市前
人中身高排名(從高到低)在全市前![]() 名的人數記為
名的人數記為![]() ,求
,求![]() 的數學期望.
的數學期望.
參考數據: ![]() ,
, ![]()
![]() ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐O﹣ABCD中,OA⊥底面ABCD,且底面ABCD是邊長為2的正方形,且OA=2,M,N分別為OA,BC的中點.
(1)求證:直線MN![]() 平面OCD;
平面OCD;
(2)求點B到平面DMN的距離.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年春節期間,某超市準備舉辦一次有獎促銷活動,若顧客一次消費達到400元則可參加一次抽獎活動,超市設計了兩種抽獎方案.
方案一:一個不透明的盒子中裝有30個質地均勻且大小相同的小球,其中10個紅球,20個白球,攪拌均勻后,顧客從中隨機抽取一個球,若抽到紅球則顧客獲得60元的返金券,若抽到白球則獲得20元的返金券,且顧客有放回地抽取3次.
方案二:一個不透明的盒子中裝有30個質地均勻且大小相同的小球,其中10個紅球,20個白球,攪拌均勻后,顧客從中隨機抽取一個球,若抽到紅球則顧客獲得80元的返金券,若抽到白球則未中獎,且顧客有放回地抽取3次.
(1)現有兩位顧客均獲得抽獎機會,且都按方案一抽獎,試求這兩位顧客均獲得180元返金券的概率;
(2)若某顧客獲得抽獎機會.
①試分別計算他選擇兩種抽獎方案最終獲得返金券的數學期望;
②為了吸引顧客消費,讓顧客獲得更多金額的返金券,該超市應選擇哪一種抽獎方案進行促銷活動?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com