【題目】如圖，已知直三棱柱
中，
，
，
是
的中點，
是
上一點，且
.
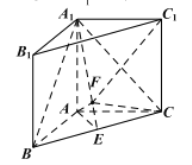
（1）證明：
平面
；
（2）求二面角
余弦值的大小.
【答案】（1）證明見解析；（2）
.
【解析】
（1）證明出
，可得出
，即有
，再證明出
平面
，可得出
，然后利用直線與平面垂直的判定定理可證明出
平面
；
（2）以點
為坐標原點，
、
、
所在直線分別為
、
、
軸建立空間直角坐標系
，然后利用空間向量法計算出二面角
余弦值的大小.
（1）由題意知，等腰直角三角形
中，中線
，且
，
在直三棱柱
中，
底面
，
、
平面，從而知
，
，
一方面，在
中，因為
，
，則
.
由
，可得
，從而可知
，又
，
則得，由此可得，即有.
另一方面，由，，
，得平面，
又
平面，則知
.
綜上，，且，又
，故平面，得證之；
（2）由題意，以點為坐標原點，、、所在直線分別為、、軸建立如下圖所示的空間直角坐標系，
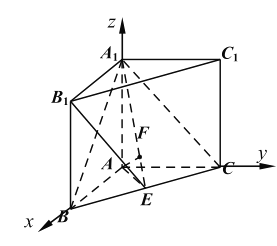
且有
、
、
、
、
，
從而有
、
、
，
由
，可得
，
記
為平面
的一個法向量，
則有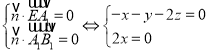
，取
，得
.
又由（1）知平面，故可取
為平面
的一個法向量，那么可得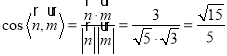
.
因此，二面角余弦值的大小為.
科目：高中數學 來源： 題型：
【題目】某商場營銷人員進行某商品M市場營銷調查發現，每回饋消費者一定的點數，該商品每天的銷量就會發生一定的變化，經過試點統計得到以如表：
反饋點數t | 1 | 2 | 3 | 4 | 5 |
銷量 |
|
| 1 |
|
|
經分析發現，可用線性回歸模型擬合當地該商品銷量
千件
與返還點數t之間的相關關系
請用最小二乘法求y關于t的線性回歸方程
，并預測若返回6個點時該商品每天銷量；
若節日期間營銷部對商品進行新一輪調整已知某地擬購買該商品的消費群體十分龐大，經營銷調研機構對其中的200名消費者的返點數額的心理預期值進行了一個抽樣調查，得到如下一份頻數表：
返還點數預期值區間
|
|
|
|
|
|
|
頻數 | 20 | 60 | 60 | 30 | 20 | 10 |
求這200位擬購買該商品的消費者對返點點數的心理預期值X的樣本平均數及中位數的估計值
同一區間的預期值可用該區間的中點值代替；估計值精確到
；
將對返點點數的心理預期值在
和
的消費者分別定義為“欲望緊縮型”消費者和“欲望膨脹型”消費者，現采用分層抽樣的方法從位于這兩個區間的30名消費者中隨機抽取6名，再從這6人中隨機抽取3名進行跟蹤調查，設抽出的3人中“欲望膨脹型”消費者的人數為隨機變量X，求X的分布列及數學期望．
參考公式及數據：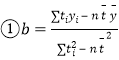
，
；
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知命題p：x∈R，2mx2+mx-
＜0，命題q：2m+1＞1．若“p∧q”為假，“p∨q”為真，則實數m的取值范圍是（ ）
A. （-3，-1）∪[0，+∞） B. （-3，-1]∪[0，+∞）
C. （-3，-1）∪（0，+∞） D. （-3，-1]∪（0，+∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設不等式組
所表示的平面區域為
，其面積為
.①若
，則
的值唯一；②若
，則的值有2個；③若為三角形，則
；④若為五邊形，則
．以上命題中，真命題的個數是( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，ABCD－A1B1C1D1是長方體，O是B1D1的中點，直線A1C交平面AB1D1于點M，則下列結論正確是( )
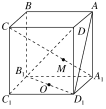
A.A，M，O三點共線B.A，M，O，A1不共面
C.A，M，C，O不共面D.B，B1，O，M共面
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖①，在等腰梯形
中，
分別為
的中點
為
中點,現將四邊形
沿
折起，使平面
平面
，得到如圖②所示的多面體，在圖②中. 
（1）證明：
；
（2）求三棱錐
的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某網絡平臺從購買該平臺某課程的客戶中，隨機抽取了100位客戶的數據，并將這100個數據按學時數，客戶性別等進行統計，整理得到如表：
學時數 |
|
|
|
|
|
|
|
男性 | 18 | 12 | 9 | 9 | 6 | 4 | 2 |
女性 | 2 | 4 | 8 | 2 | 7 | 13 | 4 |
（1）根據上表估計男性客戶購買該課程學時數的平均值（同一組中的數據用該組區間的中點值作代表，結果保留小數點后兩位）；
（2）從這100位客戶中，對購買該課程學時數在20以下的女性客戶按照分層抽樣的方式隨機抽取7人，再從這7人中隨機抽取2人，求這2人購買的學時數都不低于15的概率．
（3）將購買該課程達到25學時及以上者視為“十分愛好該課程者”，25學時以下者視，為“非十分愛好該課程者”．請根據已知條件完成以下
列聯表，并判斷是否有99．9%的把握認為“十分愛好該課程者”與性別有關？
非十分愛好該課程者 | 十分愛好該課程者 | 合計 | |
男性 | |||
女性 | |||
合計 | 100 |
附：
，
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題中，錯誤的是（ ）
A.一條直線和直線外一點確定一個平面
B.平行于同一平面的兩個不同平面平行
C.若直線
不平行平面
，則在平面內不存在與平行的直線
D.如果平面不垂直平面
，那么平面內一定不存在直線垂直于平面
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率是
，上頂點B是拋物線
的焦點.
（1）求橢圓
的標準方程；
（2）若
是橢圓上的兩個動點，且
(
是坐標原點），試問：點到直線的距離是否為定值？若是，試求出這個定值；若不是，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
