
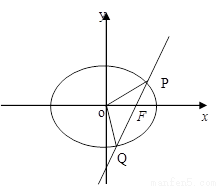
已知直線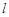 過橢圓E:
過橢圓E: 的右焦點
的右焦點 ,且與E相交于
,且與E相交于 兩點.
兩點.
(1)設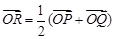 (
( 為原點),求點
為原點),求點 的軌跡方程;
的軌跡方程;
(2)若直線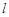 的傾斜角為
的傾斜角為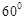 ,求
,求 的值.
的值.
(1)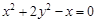 ;(2)
;(2)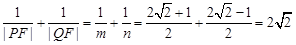
【解析】第一問中,利用向量的表達式,坐標的手段得到所求點的軌跡方程。
當直線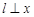 軸時,直線
軸時,直線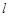 的方程是:
的方程是: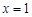 ,根據對稱性可知
,根據對稱性可知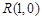
當直線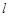 的斜率存在時,可設直線
的斜率存在時,可設直線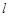 的方程為
的方程為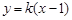
代入E有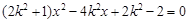
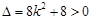 ;
; 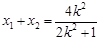
第二問中,在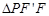 中
中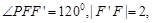 設
設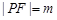 ,則
,則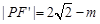
由余弦定理得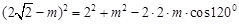
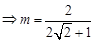
同理,在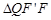 ,設
,設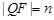 ,則
,則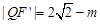
也由余弦定理得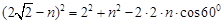
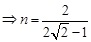
然后可得。
解:(1)設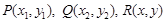
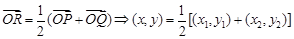
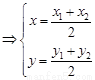
由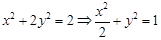 ,易得右焦點
,易得右焦點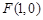 -(2分)
-(2分)
當直線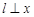 軸時,直線
軸時,直線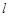 的方程是:
的方程是: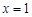 ,根據對稱性可知
,根據對稱性可知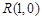
當直線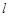 的斜率存在時,可設直線
的斜率存在時,可設直線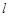 的方程為
的方程為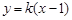
代入E有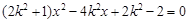
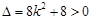 ;
; 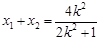 ---(5分)
---(5分)
于是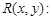
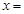
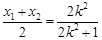 ;
; 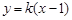
消去參數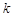 得
得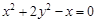 而
而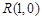 也適上式,故R的軌跡方程是
也適上式,故R的軌跡方程是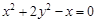 ----(8分)
----(8分)
(2)設橢圓另一個焦點為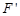 ,
,
在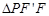 中
中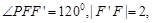 設
設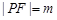 ,則
,則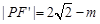
由余弦定理得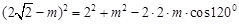
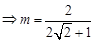
同理,在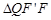 ,設
,設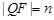 ,則
,則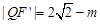
也由余弦定理得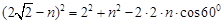
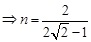
于是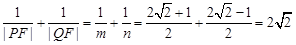 ………12分
………12分


 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com