
【題目】如圖,在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上一點(diǎn).
上一點(diǎn).
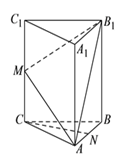
(I)求證: ![]() .
.
(II)若![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點(diǎn),求證:
的中點(diǎn),求證: ![]() ∥平面
∥平面![]() .
.
(III)若二面角![]() 的大小為
的大小為![]() ,求線段
,求線段![]() 的長
的長
【答案】(I)見解析(II)見解析(III)![]()
【解析】試題分析:
(1)∵![]() 平面
平面![]() ,∴
,∴![]() .又
.又![]() ,所以
,所以![]() 面
面![]() .從而
.從而![]() (2)欲證線面平行,轉(zhuǎn)證
(2)欲證線面平行,轉(zhuǎn)證![]() 即可,(3))以
即可,(3))以![]() 為原點(diǎn),
為原點(diǎn), ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸建立空間直角坐標(biāo)系
軸建立空間直角坐標(biāo)系![]() .
.
求出法向量,帶入公式即可.
試題解析:
(I)∵![]() 平面
平面![]() ,
, ![]() 面
面![]() ,
,
∴![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() 中,
中, ![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() 面
面![]() .
.
∵![]() 面
面![]() ,
,
∴![]() .
.
(II)連接![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() .
.
∵四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() 是
是![]() 的中點(diǎn).
的中點(diǎn).
又∵![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點(diǎn),
的中點(diǎn),
∴![]() ,且
,且![]() ,
,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() .
.
又![]() 平面
平面![]() ,
, ![]() 面
面![]() ,
,
∴![]() 平面
平面![]() .
.
(III)∵![]() ,且
,且![]() 平面
平面![]() ,
,
∴![]() ,
, ![]() ,
, ![]() 兩兩垂直。
兩兩垂直。
以![]() 為原點(diǎn),
為原點(diǎn), ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸建立空間直角坐標(biāo)系
軸建立空間直角坐標(biāo)系![]() .
.
設(shè)![]() ,則
,則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() .
.
設(shè)平面![]() 的法向量為
的法向量為![]() ,
,
故![]() ,
, ![]() ,
,
則有![]() ,令
,令![]() ,則
,則![]() ,
,
又平面![]() 的法向量為
的法向量為![]() .
.
∵二面角![]() 的大小為
的大小為![]() ,
,
∴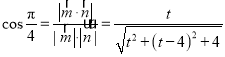 ,
,
解得![]() ,即
,即![]() ,
,
![]() ,
,
∴![]() .
.


 一線名師提優(yōu)試卷系列答案
一線名師提優(yōu)試卷系列答案 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】連接球面上兩點(diǎn)的線段稱為球的弦,半徑為4的球的兩條弦AB、CD的長度分別為2 ![]() 和4
和4 ![]() ,M、N分別是AB、CD的中點(diǎn),兩條弦的兩端都在球面上運(yùn)動,有下面四個命題:
,M、N分別是AB、CD的中點(diǎn),兩條弦的兩端都在球面上運(yùn)動,有下面四個命題:
①弦AB、CD可能相交于點(diǎn)M;
②弦AB、CD可能相交于點(diǎn)N;
③MN的最大值是5;
④MN的最小值是1;
其中所有正確命題的序號為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)不等式組 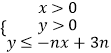 所表示的平面區(qū)域為Dn , 記Dn內(nèi)的格點(diǎn)(格點(diǎn)即橫坐標(biāo)和縱坐標(biāo)皆為整數(shù)的點(diǎn))的個數(shù)為f(n)(n∈N*).
所表示的平面區(qū)域為Dn , 記Dn內(nèi)的格點(diǎn)(格點(diǎn)即橫坐標(biāo)和縱坐標(biāo)皆為整數(shù)的點(diǎn))的個數(shù)為f(n)(n∈N*).
(1)求f(1)、f(2)的值及f(n)的表達(dá)式;
(2)設(shè)bn=2nf(n),Sn為{bn}的前n項和,求Sn;
(3)記 ![]() ,若對于一切正整數(shù)n,總有Tn≤m成立,求實(shí)數(shù)m的取值范圍.
,若對于一切正整數(shù)n,總有Tn≤m成立,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,D,E分別為AB,BC的中點(diǎn),點(diǎn)F在側(cè)棱B1B上,且B1D⊥A1F,A1C1⊥A1B1 . 求證: 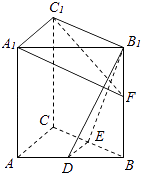
(1)直線DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知n∈N* , 設(shè)Sn是單調(diào)遞減的等比數(shù)列{an}的前n項和,a1= ![]() 且S2+a2 , S4+a4 , S3+a3成等差數(shù)列.
且S2+a2 , S4+a4 , S3+a3成等差數(shù)列.
(1)求數(shù)列{an}的通項公式;
(2)記數(shù)列{nan}的前n項和為Tn , 求證:對于任意正整數(shù)n, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)f(k)是滿足不等式log2x+log2(52k﹣1﹣x)≥2k(k∈N*)的自然數(shù)x的個數(shù).
(1)求f(k)的函數(shù)解析式;
(2)Sn=f(1)+2f(2)+…+nf(n),求Sn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】雖然吸煙有害健康,但是由于歷史以及社會的原因,吸煙也是部分公民交際的重要媒介.世界衛(wèi)生組織1987年11月建議把每年的4月7日定為世界無煙日,且從1989年開始,世界無煙日改為每年的5月31日.某報社記者專門對吸煙的市民做了戒煙方面的調(diào)查,經(jīng)抽樣只有![]() 的煙民表示愿意戒煙,將頻率視為概率.
的煙民表示愿意戒煙,將頻率視為概率.
(1)從該市吸煙的市民中隨機(jī)抽取3位,求至少有一位煙民愿意戒煙的概率;
(2)從該市吸煙的市民中隨機(jī)抽取4位, ![]() 表示愿意戒煙的人數(shù),求
表示愿意戒煙的人數(shù),求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-5:不等式選講
定義在![]() 上的函數(shù)
上的函數(shù)![]() ,若
,若![]() ,有
,有![]() ,則稱函數(shù)
,則稱函數(shù)![]() 為定義在
為定義在![]() 上的非嚴(yán)格單增函數(shù);若
上的非嚴(yán)格單增函數(shù);若![]() ,有
,有![]() ,則稱函數(shù)
,則稱函數(shù)![]() 為定義在
為定義在![]() 上的非嚴(yán)格單減函數(shù).已知:
上的非嚴(yán)格單減函數(shù).已知: ![]() .
.
(1)若函數(shù)![]() 為定義在
為定義在![]() 上的非嚴(yán)格單增函數(shù),求實(shí)數(shù)
上的非嚴(yán)格單增函數(shù),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
(2)若函數(shù)![]() 為定義在
為定義在![]() 上的非嚴(yán)格單減函數(shù),試解不等式
上的非嚴(yán)格單減函數(shù),試解不等式![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,已知向量 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),
), ![]() =(sinx,cosx),x∈(0,
=(sinx,cosx),x∈(0, ![]() ).
).
(1)若 ![]() ⊥
⊥ ![]() ,求tanx的值;
,求tanx的值;
(2)若 ![]() 與
與 ![]() 的夾角為
的夾角為 ![]() ,求x的值.
,求x的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com