【答案】
分析:(Ⅰ)把a=0代入到f(x)中化簡得到f(x)的解析式,求出f'(x),因為曲線的切點為(1,f(1)),所以把x=1代入到f'(x)中求出切線的斜率,把x=1代入到f(x)中求出f(1)的值得到切點坐標,根據切點和斜率寫出切線方程即可;
(Ⅱ)令f'(x)=0求出x的值為x=-2a和x=a-2,分兩種情況討論:①當-2a<a-2時和②當-2a>a-2時,討論f'(x)的正負得到函數的單調區間,根據函數的增減性即可得到函數的最值.
解答:(Ⅰ)解:當a=0時,f(x)=x
2e
x,f'(x)=(x
2+2x)e
x,故f'(1)=3e,
所以曲線y=f(x)在點(1,f(1))處的切線的斜率為3e,f(1)=e,
所以該切線方程為y-e=3e(x-1),
整理得:3ex-y-2e=0.
(Ⅱ)解:f'(x)=[x
2+(a+2)x-2a
2+4a]e
x令f'(x)=0,解得x=-2a,或x=a-2.由

知,-2a≠a-2.
以下分兩種情況討論.
①若a>

,則-2a<a-2.當x變化時,f'(x),f(x)的變化情況如下表:
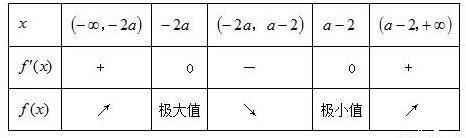
所以f(x)在(-∞,-2a),(a-2,+∞)內是增函數,在(-2a,a-2)內是減函數.
函數f(x)在x=-2a處取得極大值f(-2a),且f(-2a)=3ae
-2a.
函數f(x)在x=a-2處取得極小值f(a-2),且f(a-2)=(4-3a)e
a-2.
②若a<

,則-2a>a-2,當x變化時,f'(x),f(x)的變化情況如下表:

所以f(x)在(-∞,a-2),(-2a,+∞)內是增函數,在(a-2,-2a)內是減函數
函數f(x)在x=a-2處取得極大值f(a-2),且f(a-2)=(4-3a)e
a-2,
函數f(x)在x=-2a處取得極小值f(-2a),且f(-2a)=3ae
-2a.
點評:考查學生會利用導數求曲線上過某點切線方程的斜率,會利用導數研究函數的單調性以及根據函數的增減性得到函數的極值.靈活運用分類討論的數學思想解決數學問題.

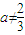 時,求函數f(x)的單調區間和極值.
時,求函數f(x)的單調區間和極值. 知,-2a≠a-2.
知,-2a≠a-2. ,則-2a<a-2.當x變化時,f'(x),f(x)的變化情況如下表:
,則-2a<a-2.當x變化時,f'(x),f(x)的變化情況如下表:
 ,則-2a>a-2,當x變化時,f'(x),f(x)的變化情況如下表:
,則-2a>a-2,當x變化時,f'(x),f(x)的變化情況如下表:


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案