(10分)如圖,PA⊥矩形ABCD所在的平面,M、N分別是AB、PC的中點.
(1)求證:MN//平面PAD
(2)求證:MN⊥CD
(3)若∠PDA=45°,求證:MN⊥平面PCD.
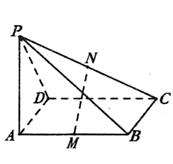
證明:(1)如圖,取PD的中點E,連結(jié)AE、EN則有EN//CD//AB//AM,
且EN=
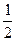
CD=
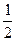
AB=MA.
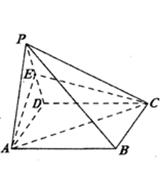
∴四邊形AMNE是平行四邊形.
∴MN//AE.
∵AE
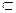
平面PAD,MN
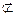
平面PAD,
∴MN//平面PAD. …………3分
(2)∵PA⊥平面ABCD,∴PA⊥AB.
又AD⊥AB,∴AB⊥平面PAD.
∴AB⊥AE,即AB⊥MN.又CD//AB,
∴MN⊥CD. …………6分
(3)∵PA⊥平面ABCD,∴PA⊥AD.
又∠PAD=45°,E是PD中點,
∴AE⊥PD,即MN⊥PD.
又MN⊥CD,∴MN⊥平面PCD.…………10分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:單選題
若直線a∥平面a,直線b⊥直線a,則直線b與平面a的位置關系是( ▲ )
| A.b∥a | B.bÌa | C.b與a相交 | D.以上均有可能 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知平面
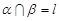
,
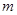
是
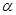
內(nèi)不同于
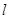
的直線,那么下列命題中錯誤的是( )
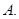
若
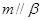
,則
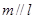
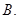
若
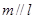
,則
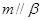
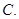
若
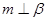
,則
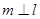
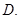
若
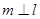
,則
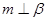
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
對于平面
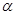
、
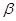
、
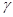
和直線
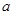
、
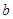
、
m、n,下列命題中真命題是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,平行四邊形

中,

,正方形

所在的平面和平面

垂直,

是

的中點,

是

的交點.

(1)求證:

平面

;
(2)求證:

平面

.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在正方體ABCD-A
1B
1C
1D
1中與AD
1成60
0角的面對角線的條數(shù)是 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分18分

)第一題滿分5分,第二題滿分5分,第三題滿分8分.
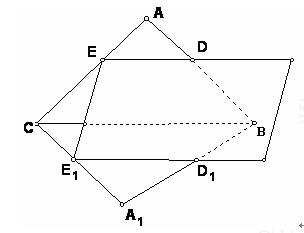
如圖,有一公共邊但不共面的兩個三角形ABC和A
1BC被一平面DEE
1D
1所截,若平面DEE
1D
1分別交AB,AC,A
1B,A
1C于點D,E,D
1,E
1。
(1)討論這三

條交線ED,CB, E
1 D
1的關系。
(2)當BC//平面DEE
1D
1時,求
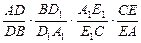
的值;
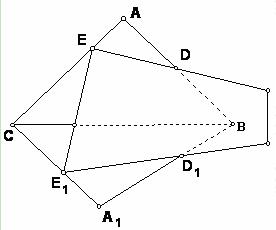
(3)當BC不平行平面DEE
1D
1時,
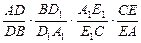
的值變化嗎?為什么?
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設
m,
n是空間兩條不同直線,
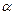
,
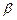
是兩個不同的平面,下面四個命題:①若
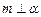
,
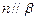
,
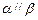
,則
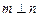
;②若
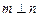
,
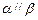
,
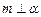
,則
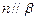
;③若
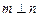
,
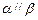
,
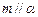
,則
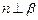
;④若
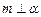
,
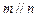
,
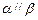
,則
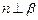
.其中正確命題的編號是
查看答案和解析>>


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 )第一題滿分5分,第二題滿分5分,第三題滿分8分.
)第一題滿分5分,第二題滿分5分,第三題滿分8分. 條交線ED,CB, E1 D1的關系。
條交線ED,CB, E1 D1的關系。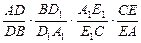 的值;
的值;
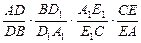 的值變化嗎?為什么?
的值變化嗎?為什么?
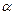 ,
,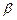 是兩個不同的平面,下面四個命題:①若
是兩個不同的平面,下面四個命題:①若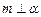 ,
,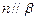 ,
,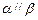 ,則
,則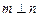 ;②若
;②若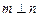 ,
,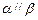 ,
,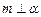 ,則
,則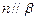 ;③若
;③若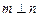 ,
,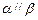 ,
,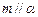 ,則
,則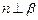 ;④若
;④若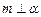 ,
,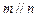 ,
,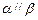 ,則
,則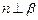 .其中正確命題的編號是
.其中正確命題的編號是