Question

2．在底面半徑為R，高為h的圓錐內有一內接圓柱，則內接圓柱的圓柱的高為$\frac{h}{2}$時，其側面積最大值為$\frac{1}{2}$πRh．

Answer 1

分析 設所求的圓柱的底面半徑為r．它的側面積S=2πrx，mh $\frac{r}{R}$=$\frac{h-x}{h}$，得r=R-$\frac{R}{h}$•x，從而得到圓柱的側面積S是關于x的二次函數S=-$\frac{2πR}{h}$x²+2πRx，由此能求出結果．

解答 解：圓錐及其內接圓柱的軸截面如圖所示．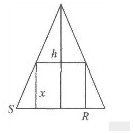
設所求的圓柱的底面半徑為r．它的側面積S=2πrx，
∵$\frac{r}{R}$=$\frac{h-x}{h}$，∴r=R-$\frac{R}{h}$•x，
∴S=2πRx-$\frac{2πR}{h}$x²，
圓柱的側面積S是關于x的二次函數：
S=-$\frac{2πR}{h}$x²+2πRx，
∵S的表達式中x²的系數小于0，
∴這個二次函數有最大值，
這時圓柱的高x=$\frac{h}{2}$，
即當圓柱的高是已知圓錐的一半時，它的側面積最大．
側面積的最大值為S_max=-$\frac{2πR}{h}•（\frac{h}{2}）^{2}$+2$πR•\frac{h}{2}$=$\frac{1}{2}πRh$．
故答案為：$\frac{h}{2}$，$\frac{1}{2}πRh$．

點評 本題考查圓錐內接圓柱的側面積的最大值的求法，是中檔題，解題時要認真審題，注意二次函數的性質的合理運用．