
如圖,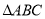 在平面
在平面 內,
內, ,AB=2BC=2,P為平面
,AB=2BC=2,P為平面 外一個動點,且PC=
外一個動點,且PC= ,
,

(1)問當PA的長為多少時,
(2)當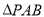 的面積取得最大值時,求直線PC與平面PAB所成角的正弦值
的面積取得最大值時,求直線PC與平面PAB所成角的正弦值
(1)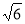 ;(2)
;(2)
【解析】
試題分析:(1)由分析可知當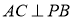 時,
時,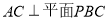 ,則
,則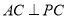 ,由勾股定理可求得
,由勾股定理可求得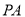 。(2)因為
。(2)因為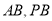 為定值,且
為定值,且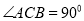 ,
,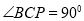 ,所以當
,所以當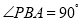 時,
時,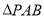 的面積取得最大值。分析可知
的面積取得最大值。分析可知 均是以
均是以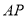 為底的等腰三角形,故取
為底的等腰三角形,故取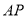 中點
中點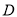 ,連接
,連接 。則有
。則有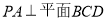 ,從而可得
,從而可得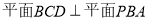 。過
。過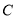 作
作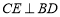 ,E為垂足,從而可得
,E為垂足,從而可得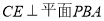 ,所以
,所以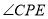 就是直線
就是直線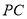 與平面
與平面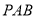 所成角,在
所成角,在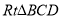 中即可求此角。
中即可求此角。
試題解析:(1)因為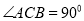 ,所以
,所以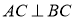 ,當
,當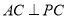 時,
時,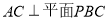 ,而
,而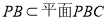 ,所以
,所以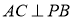 時,此時,
時,此時,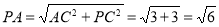 ,即當
,即當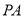 =
=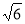 時,
時,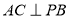
(2)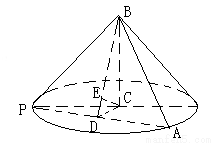
在 中,因為PC=
中,因為PC=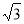 ,
,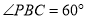 ,
,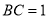 ,所以
,所以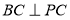 ,
,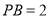 .當
.當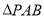 的面積取得最大值時,
的面積取得最大值時,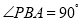 ,(如圖)在
,(如圖)在 中,因為
中,因為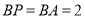 ,取
,取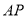 中點
中點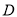 ,連接
,連接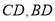 。因為
。因為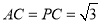 且點
且點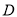 為
為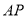 中點,所以
中點,所以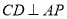 ,因為
,因為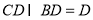 ,所以
,所以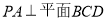 ,由此可求得
,由此可求得 ,又在
,又在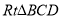 中,
中,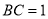 ,所以
,所以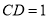 ,過
,過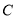 作
作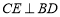 ,E為垂足,由于
,E為垂足,由于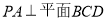 ,所以,
,所以,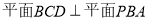 ,由兩個平面互相垂直的性質可知:
,由兩個平面互相垂直的性質可知: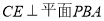 ,所以
,所以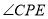 就是直線
就是直線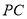 與平面
與平面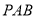 所成角,在
所成角,在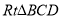 中,可求得
中,可求得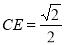 ,在
,在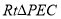 中,
中,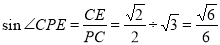 ,所以直線
,所以直線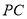 與平面
與平面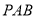 所成角的正弦值是
所成角的正弦值是 .
.
考點:1線線垂直、線面垂直;2線面角。


科目:高中數學 來源:2013-2014學年湖北省七市(州)高三年級聯合考試理科數學試卷(解析版) 題型:選擇題
閱讀如圖所示的程序框圖,則輸出結果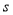 的值為( )
的值為( )

A.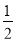 B.
B.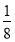 C.
C.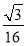 D.
D.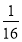
查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖北省七市(州)高三年級聯合考試文科數學試卷(解析版) 題型:選擇題
德國著名數學家狄利克雷在數學領域成就顯著,以其名命名的函數
被稱為狄利克雷函數,其中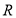 為實數集,
為實數集,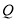 為有理數集,則關于函數
為有理數集,則關于函數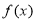 有如下四個命題:
有如下四個命題:
①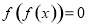 ; ②函數
; ②函數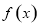 是偶函數;
是偶函數;
③任取一個不為零的有理數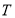 ,
,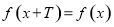 對任意的
對任意的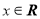 恒成立;
恒成立;
④存在三個點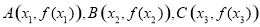 ,使得
,使得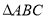 為等邊三角形.
為等邊三角形.
其中真命題的個數是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖北省七市(州)高三年級聯合考試文科數學試卷(解析版) 題型:選擇題
從裝有2個紅球和2個黑球的口袋內任取2個球,那么互斥而不對立的兩個事件是( )
A.“至少有一個黑球”與“都是黑球”
B.“至少有一個黑球”與“都是紅球”
C.“至少有一個黑球”與“至少有一個紅球”
D.“恰有一個黑球”與“恰有兩個黑球”
查看答案和解析>>
科目:高中數學 來源:2013-2014學年浙江省高三高考模擬沖刺卷(提優卷)(二)理科數學試卷(解析版) 題型:選擇題
已知雙曲線C的方程是: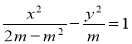 (
(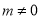 ),若雙曲線的離心率
),若雙曲線的離心率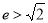 ,則實數m的取值范圍是( )
,則實數m的取值范圍是( )
A. 1<m<2. B .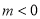 C .
C .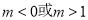 D.
D.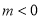 或1<m<2.
或1<m<2.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年浙江省高三高考模擬沖刺卷(提優卷)(二)文科數學試卷(解析版) 題型:填空題
某幾何體的三視圖(單位:cm)如右圖所示,則此幾何體的體積等于cm3.

查看答案和解析>>
科目:高中數學 來源:2013-2014學年浙江省高三高考模擬沖刺卷(提優卷)(三)文科數學試卷(解析版) 題型:填空題
已知定義在R上的函數f(x),g(x)滿足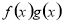 =ax,且f′(x)g(x)+ f(x)·g′(x) <0,
=ax,且f′(x)g(x)+ f(x)·g′(x) <0,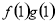 +
+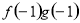 =
=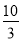 ,若有窮數列{
,若有窮數列{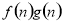 }(n∈N*)的前n項和等于
}(n∈N*)的前n項和等于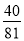 ,則n等于 .
,則n等于 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com