
【題目】已知橢圓![]() 的離心率
的離心率![]() ,橢圓上的點到左焦點
,橢圓上的點到左焦點![]() 的距離的最大值為
的距離的最大值為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)已知直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點.在
兩點.在![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() 且
且![]() ,若存在,求出實數
,若存在,求出實數![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源: 題型:
【題目】已知![]() ,命題
,命題![]() 方程
方程![]() 表示焦點在
表示焦點在![]() 軸上的橢圓,命題
軸上的橢圓,命題![]() 方程
方程![]() 表示雙曲線.
表示雙曲線.
(1)若命題![]() 是真命題,求實數
是真命題,求實數![]() 的范圍;
的范圍;
(2)若命題“![]() 或
或![]() ”為真命題,“
”為真命題,“![]() 且
且![]() ”是假命題,求實數
”是假命題,求實數![]() 的范圍.
的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() =1(a>b>0),F1、F2分別為橢圓的左、右焦點,A為橢圓的上頂點,直線AF2交橢圓于另一點B.
=1(a>b>0),F1、F2分別為橢圓的左、右焦點,A為橢圓的上頂點,直線AF2交橢圓于另一點B.
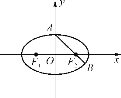
(1)若∠F1AB=90°,求橢圓的離心率;
(2)若![]() =2
=2![]() ,
,![]() ·
·![]() =
=![]() ,求橢圓的方程.
,求橢圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設有一組圓![]() .下列四個命題正確的是( )
.下列四個命題正確的是( )
A. 存在![]() ,使圓與
,使圓與![]() 軸相切
軸相切
B. 存在一條直線與所有的圓均相交
C. 存在一條直線與所有的圓均不相交
D. 所有的圓均不經過原點
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某海產品經銷商調查發現,該海產品每售出![]() 噸可獲利
噸可獲利![]() 萬元,每積壓
萬元,每積壓![]() 噸則虧損
噸則虧損![]() 萬元.根據往年的數據,得到年需求量的頻率分布直方圖如圖所示,將頻率視為概率.
萬元.根據往年的數據,得到年需求量的頻率分布直方圖如圖所示,將頻率視為概率.
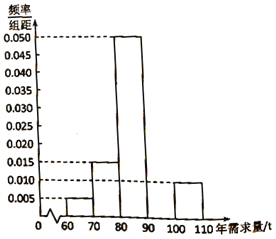
(1)請補齊![]() 上的頻率分布直方圖,并依據該圖估計年需求量的平均數;
上的頻率分布直方圖,并依據該圖估計年需求量的平均數;
(2)今年該經銷商欲進貨![]() 噸,以
噸,以![]() (單位:噸,
(單位:噸, ![]() )表示今年的年需求量,以
)表示今年的年需求量,以![]() (單位:萬元)表示今年銷售的利潤,試將
(單位:萬元)表示今年銷售的利潤,試將![]() 表示為
表示為![]() 的函數解析式;并求今年的年利潤不少于
的函數解析式;并求今年的年利潤不少于![]() 萬元的概率.
萬元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 依法納稅是每個公民應盡的義務,個人取得的所得應依照《中華人民共和國個人所得稅法》向國家繳納個人所得稅(簡稱個稅).![]() 年
年![]() 月
月![]() 日起,個稅稅額根據應納稅所得額、稅率和速算扣除數確定,計算公式為:個稅稅額=應納稅所得額×稅率-速算扣除數.①應納稅所得額的計算公式為:應納稅所得額=綜合所得收入額-基本減除費用-專項扣除-專項附加扣除-依法確定的其他扣除.②其中,“基本減除費用”(免征額)為每年
日起,個稅稅額根據應納稅所得額、稅率和速算扣除數確定,計算公式為:個稅稅額=應納稅所得額×稅率-速算扣除數.①應納稅所得額的計算公式為:應納稅所得額=綜合所得收入額-基本減除費用-專項扣除-專項附加扣除-依法確定的其他扣除.②其中,“基本減除費用”(免征額)為每年![]() 元.稅率與速算扣除數見下表.
元.稅率與速算扣除數見下表.
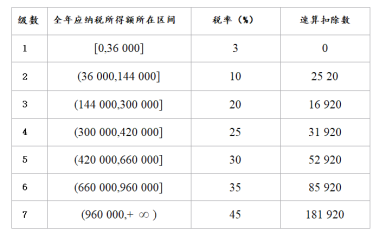
(1)設全年應納稅所得額為![]() ,應繳納個稅稅額為
,應繳納個稅稅額為![]() ,求
,求![]() 的解析式;
的解析式;
(2)小李全年綜合所得收入額為![]() 元,假定繳納的基本養老保險、基本醫療保險、失業保險等社會保險費和住房公積金占綜合所得收入額的比例分別是
元,假定繳納的基本養老保險、基本醫療保險、失業保險等社會保險費和住房公積金占綜合所得收入額的比例分別是![]() ,
,![]() ,
,![]() ,
,![]() ,專項附加扣除是
,專項附加扣除是![]() 元,依法確定其他扣除是
元,依法確定其他扣除是![]() 元,那么他全年應繳納多少綜合所得個稅?
元,那么他全年應繳納多少綜合所得個稅?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某種藥物在血液中以每小時![]() 的比例衰減,現給某病人靜脈注射了該藥物2500mg,設經過x個小時后,藥物在病人血液中的量為ymg.
的比例衰減,現給某病人靜脈注射了該藥物2500mg,設經過x個小時后,藥物在病人血液中的量為ymg.
![]() 與x的關系式為______;
與x的關系式為______;
![]() 當該藥物在病人血液中的量保持在1500mg以上,才有療效;而低于500mg,病人就有危險,要使病人沒有危險,再次注射該藥物的時間不能超過______小時
當該藥物在病人血液中的量保持在1500mg以上,才有療效;而低于500mg,病人就有危險,要使病人沒有危險,再次注射該藥物的時間不能超過______小時![]() 精確到
精確到![]() .
.
![]() 參考數據:
參考數據:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com