
設二次函數 在[-1,4]上的最大值為12,且關于x的不等式
在[-1,4]上的最大值為12,且關于x的不等式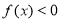 的解集為(0,5).
的解集為(0,5).
(1)求 的解析式;
的解析式;
(2)若對任意的實數x都有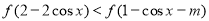 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.
(1) ;(2)
;(2)
【解析】
試題分析:(1)二次函數在閉區間上的最值主要有三種類型:軸定區間定、軸動區間定、軸定區間動,不論哪種類型,解題的關鍵是對稱軸與區間的關系,當含有參數時,要依據對稱軸與區間的關系進行分類討論;(2)二次函數、二次方程與二次不等式統稱“三個”二次,它們常結合在一起,有關二次函數的問題,數形結合,密切聯系圖象是探求解題思路的有效方法,一般從:①開口方向;②對稱軸位置;③判別式;④端點值符合四個方面分析;(3)二次函數的綜合問題應用多涉及單調性與最值或二次方程根的分布問題,解決的主要思路是等價轉化,多用到數形結合思想與分類討論思想
試題解析:解:(1)依題意可設二次函數的解析式為f(x)=ax(x-5)且a>0,則
∴f(x)=ax(x-5)=a(x-2.5)2-6.25a
又∵f(x)在[-1,4]上的最大值為12
∴6a=12 ? a=2
∴
(2)解法一:設t=1-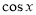 ,則0≤t≤2
,則0≤t≤2
∴f(2-2cosx)<f(1-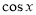 -m)
-m)
?2·2t·(2t-5)<2·(t-m)·(t-m-5)
?(3t-m-5)(t+m)<0

∴實數m的取值范圍為
解法二:因為f(x)的對稱軸為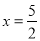 且其圖象開口向上
且其圖象開口向上
所以f(2-2cosx)<f(1-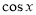 -m)等價于
-m)等價于
|2-2cosx-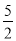 |<|1-
|<|1-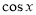 -m-
-m-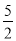 | 即|2cosx+
| 即|2cosx+ |<|
|<|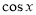 +m+
+m+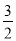 |
|
令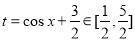 即|2t-
即|2t-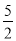 |<|t+m|
|<|t+m|

∴實數m的取值范圍為 .
.
考點:(1)求二次函數的解析式;(2)恒成立的問題


科目:高中數學 來源:2015屆浙江省富陽市高二下學期期中考試理科數學試卷(解析版) 題型:選擇題
函數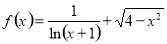 的定義域為( ).
的定義域為( ).
A.[-2,0)∪(0,2] B.(-1,0)∪(0,2] C.[-2,2] D.(-1,2]
查看答案和解析>>
科目:高中數學 來源:2015屆浙江富陽二中高二下學期第三次質量檢測理科數學試卷(解析版) 題型:填空題
已知△ 中,
中, ,它所在平面外一點
,它所在平面外一點 到△
到△ 三個頂
三個頂
點的距離都是14,那么點P到平面ABC的距離為______
查看答案和解析>>
科目:高中數學 來源:2015屆浙江富陽二中高二下學期第三次質量檢測理科數學試卷(解析版) 題型:選擇題
.過雙曲線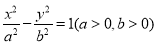 的左頂點
的左頂點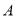 作與實軸垂直的直線,交兩漸近線于
作與實軸垂直的直線,交兩漸近線于 ,
, 兩點,
兩點,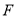 為該雙曲線的右焦點,若△
為該雙曲線的右焦點,若△ 的內切圓恰好是
的內切圓恰好是 ,則該雙曲線的離心率為( )
,則該雙曲線的離心率為( )
A.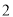 B.
B. C.
C.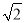 D.
D.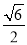
查看答案和解析>>
科目:高中數學 來源:2015屆河南省頂級名校高三入學定位考試文科數學試卷(解析版) 題型:解答題
如圖, 四棱柱 的底面ABCD是正方形, O為底面中心,
的底面ABCD是正方形, O為底面中心,  ⊥平面ABCD,
⊥平面ABCD,  .
.
(1)證明:  // 平面
// 平面 ;
;
(2)求三棱柱 的體積.
的體積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com