
【題目】已知:在平面四邊形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() (如圖1),若將
(如圖1),若將![]() 沿對角線BD折疊,使
沿對角線BD折疊,使![]() (如圖2).請在圖2中解答下列問題.
(如圖2).請在圖2中解答下列問題.
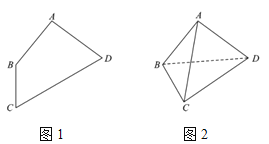
(1)證明:![]() ;
;
(2)求三棱錐![]() 的高.
的高.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)在圖1中,根據平面幾何知識可得BC=1且∠CBD=90°,在圖2中可以得到AC2=AB2+CB2,從而可證明BC⊥平面ABD從而可證明結論.
(2)由(1)有![]() ,用等體積法有
,用等體積法有![]() .
.
證明:法1:由左圖知,![]()
在△BDC中,∠CBD=135°-45°=90°,
∠BDC=75°-45°=30°,
![]() ,所以BC=1,
,所以BC=1,
又在右圖中,因為AC![]() ,AB=AD
,AB=AD![]() ,所以AC2=AB2+CB2
,所以AC2=AB2+CB2
所以BC⊥AB
又因為∠CBD=90°,所以BC⊥平面ABD
所以BC⊥AD
法2:如右圖,設BD的中點為O,連結A0,CO,因為∠A=90°,AB=AD![]()
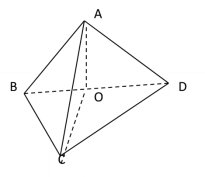
則![]()
由左圖知,在△BDC中,∠CBD=135°-45°=90°
∠BDC=75°-45°=30°,所以BC=1,所以![]()
又因為AC![]() ,所以AC2=AO2+CO2
,所以AC2=AO2+CO2
所以AO⊥CO,所以AO⊥平面BCD,所以平面ABD⊥平面BCD,又∠CBD=90°
所以BC⊥平面ABD, 所以BC⊥AD
(2)因為AB=AD![]() ,AC
,AC![]() ,CD2=BC2+BD2=4
,CD2=BC2+BD2=4
所以CD2=AC2+AD2,所以AC⊥AD
設三棱錐B-ADC的高為h,則
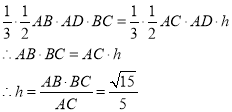


 全能測控一本好卷系列答案
全能測控一本好卷系列答案 發散思維新課堂系列答案
發散思維新課堂系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率
,離心率![]() ,點
,點![]() 是橢圓上的一個動點,
是橢圓上的一個動點,![]() 面積的最大值是
面積的最大值是![]() .
.
(1)求橢圓的方程;
(2)若![]() 是橢圓上不重合的四點,
是橢圓上不重合的四點,![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() ,且
,且![]() ,求此時直線
,求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)設![]() ,求函數
,求函數![]() 在區間
在區間![]() 上的最小值;
上的最小值;
(3)某同學發現:總存在正實數![]() ,
,![]() ,使
,使![]() ,試問:該同學的判斷是否正確?若不正確,請說明理由;若正確,請直接寫出
,試問:該同學的判斷是否正確?若不正確,請說明理由;若正確,請直接寫出![]() 的取值范圍(不需要解答過程).
的取值范圍(不需要解答過程).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人的月工資由基礎工資和績效工資組成2010年每月的基礎工資為2100元、績效工資為2000元從2011年起每月基礎工資比上一年增加210元、績效工資為上一年的![]() 照此推算,此人2019年的年薪為______萬元(結果精確到
照此推算,此人2019年的年薪為______萬元(結果精確到![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的質量以其質量指標值來衡量,質量指標值越大表明質量越好,記其質量指標值為![]() ,當
,當![]() 時,產品為一級品;當
時,產品為一級品;當![]() 時,產品為二級品,當
時,產品為二級品,當![]() 時,產品為三級品,現用兩種新配方(分別稱為
時,產品為三級品,現用兩種新配方(分別稱為![]() 配方和
配方和![]() 配方)做實驗,各生產了
配方)做實驗,各生產了![]() 件這種產品,并測量了每件產品的質量指標值,得到下面的試驗結果 :(以下均視頻率為概率)
件這種產品,并測量了每件產品的質量指標值,得到下面的試驗結果 :(以下均視頻率為概率)
![]() 配方的頻數分配表:
配方的頻數分配表:
指標值分組 |
|
|
|
|
頻數 |
|
|
|
|
![]() 配方的頻數分配表:
配方的頻數分配表:
指標值分組 |
|
|
|
|
|
頻數 |
|
|
|
|
|
(1)若從![]() 配方產品中有放回地隨機抽取
配方產品中有放回地隨機抽取![]() 件,記“抽出的
件,記“抽出的![]() 配方產品中至少
配方產品中至少![]() 件二級品”為事件
件二級品”為事件![]() ,求事件
,求事件![]() 發生的概率
發生的概率![]() ;
;
(2)若兩種新產品的利潤率![]() 與質量指標
與質量指標![]() 滿足如下關系:
滿足如下關系: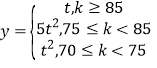 ,其中
,其中![]() ,從長期來看,投資哪種配方的產品平均利潤率較大?
,從長期來看,投資哪種配方的產品平均利潤率較大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從5名男生和4名女生中選出4人參加辯論比賽.
(1)如果男生中的甲與女生中的乙至少要有1人在內,那么有多少種不同選法?
(2)如果4個人中既有男生又有女生,那么有多少種不同選法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為提高衡水市的整體旅游服務質量,市旅游局舉辦了旅游知識競賽,參賽單位為本市內各旅游協會,參賽選手為持證導游.現有來自甲旅游協會的導游3名,其中高級導游2名;乙旅游協會的導游3名,其中高級導游1名.從這6名導游中隨機選擇2人參加比賽.
(1)求選出的2名都是高級導游的概率;
(2)為了進一步了解各旅游協會每年對本地經濟收入的貢獻情況,經多次統計得到,甲旅游協會對本地經濟收入的貢獻范圍是![]() (單位:萬元),乙旅游協會對本地經濟收入的貢獻范圍是
(單位:萬元),乙旅游協會對本地經濟收入的貢獻范圍是![]() (單位:萬元),求甲旅游協會對本地經濟收入的貢獻不低于乙旅游協會對本地經濟收入的貢獻概率.
(單位:萬元),求甲旅游協會對本地經濟收入的貢獻不低于乙旅游協會對本地經濟收入的貢獻概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數y=f(x),若在其定義域內存在x0,使得x0f(x0)=1成立,則稱函數f(x)具有性質M.
(1)下列函數中具有性質M的有____
①f(x)=﹣x+2
②f(x)=sinx(x∈[0,2π])
③f(x)=x![]() ,(x∈(0,+∞))
,(x∈(0,+∞))
④f(x)![]()
(2)若函數f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性質M,則實數a的取值范圍是____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com