設等差數列
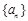
的前
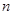
項和為
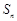
,滿足:
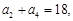
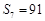
.遞增的等比數列
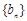
前
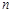
項和為
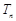
,滿足:
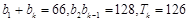
.
(Ⅰ)求數列
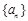
,
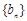
的通項公式;
(Ⅱ)設數列
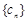
對
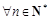
,均有
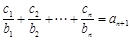
成立,求
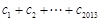
.
試題分析:(Ⅰ)先由等差數列
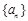
的性質得出
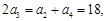
從而求出
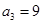
,再結合
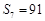
求出
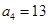
,從而得出
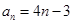
;由
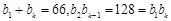
,可構造方程
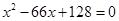
,從而求出

,由
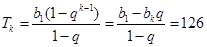
求出
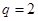
,故
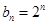
;(Ⅱ)當
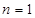
時,
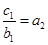
求得
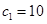
;當
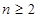
時由
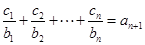
,
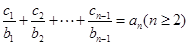
,作差可得
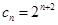
,故
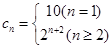
,從而可求

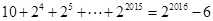
.
試題解析:(Ⅰ)由題意
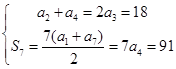
得

,則
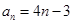
2分
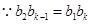
,
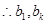
方程
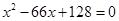
的兩根,得

4分
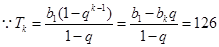
,

代入求得
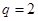
,

6分
(Ⅱ)由
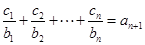
,
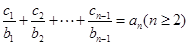
兩式相減有

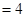
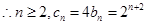
,9分
又
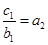
,得
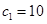
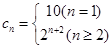
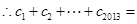
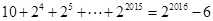
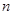
項和
練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:解答題
已知數列
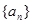
的前
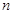
項的和為
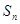
,
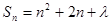
,求證:數列
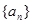
為等差數列的充要條件是
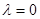
.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
設等比數列
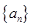
的首項為
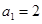
,公比為
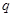
(
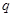
為正整數),且滿足
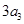
是
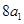
與
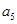
的等差中項;數列
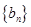
滿足
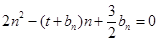
(
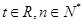
).
(1)求數列
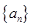
的通項公式;
(2)試確定
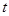
的值,使得數列
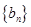
為等差數列;
(3)當
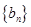
為等差數列時,對每個正整數
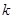
,在
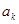
與
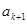
之間插入
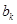
個2,得到一個新數列
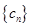
. 設
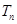
是數列
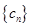
的前
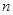
項和,試求滿足
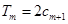
的所有正整數
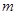
.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知
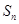
為等差數列
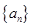
的前
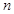
項和,且
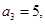
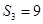
.
(Ⅰ)求
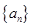
的通項公式;
(Ⅱ)求數列
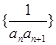
的前
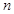
項和
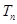
.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
已知等差數列
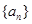
的公差為2,若
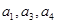
成等比數列,則a
2=( )
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
在數列
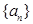
中,
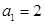
,
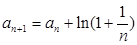
,則

=( )
| A.2+(n-1)lnn | B.2+lnn | C.2+nlnn | D.1+n+lnn |
查看答案和解析>>
主站蜘蛛池模板:
久久一区二区视频
|
亚洲国产精品99久久久久久久久
|
91精品一区二区三区在线观看
|
欧美女优在线视频
|
99久久免费精品国产男女性高好
|
国产精品1区2区
|
久草在线青青草
|
99视频精品|
日本在线观看一区二区
|
热久久久久
|
国产探花在线精品一区二区
|
91精品国产综合久久久蜜臀粉嫩
|
超碰人人干
|
在线免费观看黄色
|
日韩一区在线播放
|
在线观看你懂的视频
|
成人精品久久久
|
国产精品一区欧美
|
久久久精品欧美一区二区免费
|
欧美淫视频
|
免费av在线播放
|
91在线免费看
|
国产欧美精品一区二区三区四区
|
久久激
|
yellow在线免费观看
|
久久99国产精品久久99果冻传媒
|
亚洲欧美日韩精品久久亚洲区
|
日韩一区二区不卡
|
欧美另类一区二区
|
亚州av|
一卡二卡久久
|
免费一级毛片
|
日韩一二三区
|
欧美在线视频一区二区
|
国产伦精品一区二区三毛
|
www.久久久
|
欧美freesex交免费视频
|
毛片毛片毛片毛片毛片毛片毛片毛片
|
日韩视频一区二区
|
国产精品一区二区欧美
|
天堂av中文在线
|

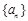 的前
的前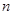 項和為
項和為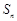 ,滿足:
,滿足: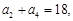
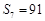 .遞增的等比數列
.遞增的等比數列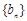 前
前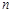 項和為
項和為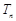 ,滿足:
,滿足: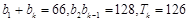 .
.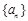 ,
,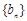 的通項公式;
的通項公式;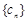 對
對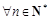 ,均有
,均有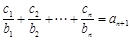 成立,求
成立,求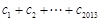 .
. 53隨堂測系列答案
53隨堂測系列答案 的首項為
的首項為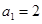 ,公比為
,公比為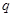 (
(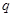 為正整數),且滿足
為正整數),且滿足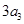 是
是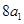 與
與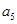 的等差中項;數列
的等差中項;數列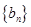 滿足
滿足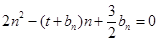 (
(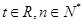 ).
).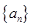 的通項公式;
的通項公式;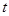 的值,使得數列
的值,使得數列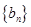 為等差數列;
為等差數列;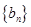 為等差數列時,對每個正整數
為等差數列時,對每個正整數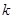 ,在
,在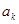 與
與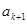 之間插入
之間插入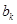 個2,得到一個新數列
個2,得到一個新數列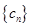 . 設
. 設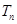 是數列
是數列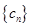 的前
的前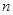 項和,試求滿足
項和,試求滿足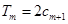 的所有正整數
的所有正整數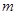 .
.