Question

由動點P向圓x²+y²=1引兩條切線PA、PB，切點分別為A、B，∠APB=60°，則動點P的軌跡方程為    ．

Answer 1

【答案】分析：先設點P的坐標為（x，y），則可得|PO|，根據∠APB=60°可得∠AP0=30°，判斷出|PO|=2|OB|，把|PO|代入整理后即可得到答案．
解答：解：設點P的坐標為（x，y），則|PO|=
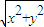
∵∠APB=60°
∴∠AP0=30°
∴|PO|=2|OB|=2
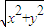
∴=2
即x²+y²=4
故答案為：x²+y²=4
點評：本題主要考查了求軌跡方程的問題．屬基礎題．