
【題目】已知函數f(x)=﹣ ![]() x2+(a﹣1)x+lnx.
x2+(a﹣1)x+lnx.
(1)若a>﹣1,求函數f(x)的單調區間;
(2)若g(x)= ![]() x2+(1﹣2a)x+f(x)有且只有兩個零點,求實數a的取值范圍.
x2+(1﹣2a)x+f(x)有且只有兩個零點,求實數a的取值范圍.
【答案】
(1)解:f(x)=﹣ ![]() x2+(a﹣1)x+lnx,(x>0),
x2+(a﹣1)x+lnx,(x>0),
f′(x)=﹣ax+(a﹣1)+ ![]() =
= ![]() ,
,
0<﹣a<1即﹣1<a<0時,﹣ ![]() >1,
>1,
令f′(x)>0,解得:x>﹣ ![]() 或0<x<1,
或0<x<1,
令f′(x)<0,解得:1<x<﹣ ![]() ,
,
∴f(x)在(0,1)遞增,在(1,﹣ ![]() )遞減,在(﹣
)遞減,在(﹣ ![]() ,+∞)遞增,
,+∞)遞增,
﹣a≤0即a≥0時,﹣ax﹣1<0,
令f′(x)>0,解得:0<x<1,令f′(x)<0,解得:x>1,
∴f(x)在(0,1)遞增,在(1,+∞)遞減;
(2)解:若g(x)= ![]() x2+(1﹣2a)x+f(x)有且只有兩個零點,
x2+(1﹣2a)x+f(x)有且只有兩個零點,
即lnx=ax有且只有兩個零點,
即h(x)=lnx,y=ax有且只有2個交點,
由h(x)=lnx的圖象與直線y=ax有兩交點
可知;a>0,
當直線與h(x)=lnx相切時,設切點(x0,lnx0)
∵h′(x)= ![]() ,
,
∴根據切線的斜率與導數值的關系可知: ![]() =a,即x0=
=a,即x0= ![]() ,
,
代入直線方程可得;ln ![]() =1,解得:a=
=1,解得:a= ![]() ,
,
所以函數h(x)=lnx的圖象與直線y=ax有兩交點,
則0<a< ![]()
【解析】(1)求出函數的導數,通過討論a的范圍,解關于導函數的不等式,求出函數的單調區間即可;(2)由h(x)=lnx的圖象與直線y=ax有兩交點可知;a>0,再根據導數求出切線的斜率,即可求出有2個交點時a的范圍.
【考點精析】本題主要考查了利用導數研究函數的單調性的相關知識點,需要掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減才能正確解答此題.
在這個區間單調遞減才能正確解答此題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某市教育局委托調查機構對本市中小學學校使用“微課掌上通”滿意度情況進行調查.隨機選擇小學和中學各50所學校進行調查,調查情況如表:
評分等級 | ☆ | ☆☆ | ☆☆☆ | ☆☆☆☆ | ☆☆☆☆☆ |
小學 | 2 | 7 | 9 | 20 | 12 |
中學 | 3 | 9 | 18 | 12 | 8 |
(備注:“☆”表示評分等級的星級,例如“☆☆☆”表示3星級.)
(1)從評分等級為5星級的學校中隨機選取兩所學校,求恰有一所學校是中學的概率;
(2)規定:評分等級在4星級以上(含4星)為滿意,其它星級為不滿意.完成下列2×2列聯表并幫助判斷:能否在犯錯誤的概率不超過0.05的前提下認為使用是否滿意與學校類別有關系?
學校類型 | 滿意 | 不滿意 | 總計 |
小學 | 50 | ||
中學 | 50 | ||
總計 | 100 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程
(Ⅰ)若圓x2+y2=4在伸縮變換![]() (λ>0)的作用下變成一個焦點在x軸上,且離心率為
(λ>0)的作用下變成一個焦點在x軸上,且離心率為![]() 的橢圓,求λ的值;
的橢圓,求λ的值;
(Ⅱ)在極坐標系中,已知點A(2,0),點P在曲線C:ρ=![]() 上運動,求P、A兩點間的距離的最小值.
上運動,求P、A兩點間的距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于集合A={x|x=m2﹣n2 , m∈Z,n∈Z},因為16=52﹣32 , 所以16∈A,研究下列問題:
(1)1,2,3,4,5,6六個數中,哪些屬于A,哪些不屬于A,為什么?
(2)討論集合B={2,4,6,8,…,2n,…}中有哪些元素屬于A,試給出一個普通的結論,不必證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=1+2sinxcosx+2cos2x.
(1)求f(x)遞增區間;
(2)求f(x)的對稱軸方程;
(3)求f(x)的最大值并寫出取最大值時自變量x的集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l: 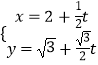 (t為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρ=2.
(t為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρ=2.
(1)若點M的直角坐標為(2, ![]() ),直線l與曲線C交于A、B兩點,求|MA|+|MB|的值;
),直線l與曲線C交于A、B兩點,求|MA|+|MB|的值;
(2)設曲線C經過伸縮變換 ![]() 得到曲線C′,求曲線C′的內接矩形周長的最大值.
得到曲線C′,求曲線C′的內接矩形周長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的分數三角形,稱為“萊布尼茨三角形”.這個三角形的規律是:各行中的每一個數,都等于后面一行中與它相鄰的兩個數之和(例如第4行第2個數 ![]() 等于第5行中的第2個數
等于第5行中的第2個數 ![]() 與第3個數
與第3個數 ![]() 之和).則
之和).則
在“萊布尼茨三角形”中,第10行從左到右第2個數到第8個數中各數的倒數之和為( )
A.5010
B.5020
C.10120
D.10130
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋中共有15個除了顏色外完全相同的球,其中有10個白球,5個紅球.從袋中任取2個球,所取的2個球中恰有1個白球,1個紅球的概率為( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com