
(1)求證:AB1D⊥平面ABB1A1;
(2)求點C到平面AB1D的距離;
(3)求平面AB1D與平面ABC所成二面角(銳角)的大小.
(1)證明:取AB1中點M,則![]() =
=![]() +
+![]() +
+![]() .?
.?
又![]() =
=![]() +
+![]() +
+![]() ,
,
兩式相加可得2![]() =
=![]() +
+![]() =
=![]() +
+![]() .?
.?
由于2![]() ·
·![]() =(
=(![]() +
+![]() )·
)·![]() =0,
=0,
2![]() ·
·![]() =(
=(![]() +
+![]() )·(
)·(![]() -
-![]() )=|
)=|![]() |2-|
|2-|![]() |2=0.
|2=0.
∴DM⊥AA1,DM⊥AB.
∴DM⊥平面ABB1A1,而DM![]() 平面AB1D.
平面AB1D.
∴平面AB1D⊥平面ABB1A1.
(2)解析:一方面A1B⊥DM,另一方面
![]() ·
·![]() =(
=(![]() -
-![]() )·(
)·(![]() +
+![]() )=|
)=|![]() |2-|
|2-|![]() |2=0,
|2=0,
∴A1B⊥AB1.∴A1B⊥平面AB1D.
∴A1B是平面AB1D的法向量.
∴C點到平面AB1D的距離d=|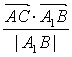 |=
|=![]() =
=![]() =
=![]() .?
.?
(3)解析:平面![]() C的法向量為
C的法向量為![]() ,而平面AB1D的法向量是
,而平面AB1D的法向量是![]() ,設所求二面角為θ(銳角),則
,設所求二面角為θ(銳角),則
|cos(π-θ)|=|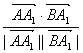 |
|
=|![]() |=
|=![]() =
=![]() .?
.?
∴θ=45°.


科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,三棱柱ABC-A1B1C1的側棱AA2⊥底面ABC,∠ACB=90°,E是棱CC1的中點,F是AB中點,AC=BC=1,AA1=1.
如圖,三棱柱ABC-A1B1C1的側棱AA2⊥底面ABC,∠ACB=90°,E是棱CC1的中點,F是AB中點,AC=BC=1,AA1=1.查看答案和解析>>
科目:高中數學 來源: 題型:
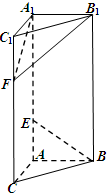 (2013•閔行區二模)如圖,在直三棱柱ABC-A1B1C1中,∠BAC=
(2013•閔行區二模)如圖,在直三棱柱ABC-A1B1C1中,∠BAC=| π | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
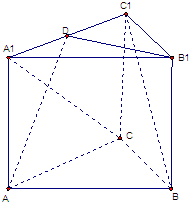 (2008•南京二模)如圖,已知正三棱柱ABC-A1B1C1中,AB=
(2008•南京二模)如圖,已知正三棱柱ABC-A1B1C1中,AB=| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com