
【題目】定義在![]() 上的函數
上的函數![]() 滿足
滿足![]() ,
,![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)求函數![]() 的單調區間;
的單調區間;
(3)如果![]() 、
、![]() 、
、![]() 滿足
滿足![]() ,那么稱
,那么稱![]() 比
比![]() 更靠近
更靠近![]() .當
.當![]() 且
且![]() 時,試比較
時,試比較![]() 和
和![]() 哪個更靠近
哪個更靠近![]() ,并說明理由.
,并說明理由.
【答案】(1)![]() ;
;
(2)當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ;當
;當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;
(3)![]() 比
比![]() 更靠近
更靠近![]() .
.
【解析】
試題分析:(1)兩邊求導,可建立關于![]() ,
,![]() 的方程組,求得其值,即可得到解析式;(2)求導,對
的方程組,求得其值,即可得到解析式;(2)求導,對![]() 的取值進行分類討論,即可得到結論;(3)設
的取值進行分類討論,即可得到結論;(3)設![]() ,
,![]() ,從而問題等價于
,從而問題等價于![]() ,通過對
,通過對![]() 的取值范圍進行分類討論,利用求導判斷單調性求極值,即可得到結論.
的取值范圍進行分類討論,利用求導判斷單調性求極值,即可得到結論.
試題解析:(1)![]() ,∴
,∴![]() ,即
,即![]() ,又
,又![]() ,∴
,∴![]() ,∴
,∴![]() ;(2)∵
;(2)∵![]() ,
,
∴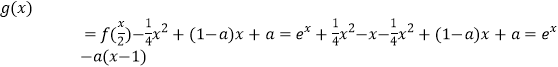 ,
,
∴![]() ,①當
,①當![]() 時,
時,![]() ,函數
,函數![]() 在
在![]() 上單調遞增,②當
上單調遞增,②當![]() 時,由
時,由![]() 得
得![]() ,∴
,∴![]() 時,
時,![]() ,
,![]() 單調遞減;
單調遞減;![]() 時,
時,![]() ,
,![]() 單調遞增,綜上,當
單調遞增,綜上,當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ;當
;當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ;(3)設
;(3)設![]() ,
,![]() ,∵
,∵![]() ,∴
,∴![]() 在
在![]() 上為減函數,又∵
上為減函數,又∵![]() ,
,
∴當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() 在
在![]() 上為增函數,又∵
上為增函數,又∵![]() ,∴
,∴![]() 時,
時,![]() ,∴
,∴![]() 在
在![]() 上為增函數,∴
上為增函數,∴![]() ,①當
,①當![]() 時,
時,![]() ,
,
設![]() ,則
,則![]() ,∴
,∴![]() 在
在![]() 上為減函數,
上為減函數,
∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() 比
比![]() 更靠近
更靠近![]() ,
,
②當![]() 時,
時,![]() ,
,
設![]() ,則
,則![]() ,
,![]() ,∴
,∴![]() 在
在![]() 時為減函數,
時為減函數,
∴![]() ,∴
,∴![]() 在
在![]() 時為減函數,∴
時為減函數,∴![]() ,
,
∴![]() ,∴
,∴![]() 比
比![]() 更靠近
更靠近![]() ,綜上:在
,綜上:在![]() ,
,![]() 時,
時,![]() 比
比![]() 更靠近
更靠近![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]()
![]() 在
在![]() 時有最大值
時有最大值![]() 和最小值
和最小值![]() ,設
,設![]() .
.
(1)求實數![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)若關于![]() 的方程
的方程![]() 有三個不同的實數解,求實數
有三個不同的實數解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐![]() (如圖一)的平面展開圖(如圖二)中,四邊形
(如圖一)的平面展開圖(如圖二)中,四邊形![]() 為邊長等于
為邊長等于![]() 的正方形,
的正方形,![]() 和
和![]() 均為正三角形,在三棱錐
均為正三角形,在三棱錐![]() 中:
中:
(I)證明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若點![]() 在棱
在棱![]() 上運動,當直線
上運動,當直線![]() 與平面
與平面![]() 所成的角最大時,求二面角
所成的角最大時,求二面角![]() 的余弦值.
的余弦值.

圖一

圖二
查看答案和解析>>
科目:高中數學 來源: 題型:
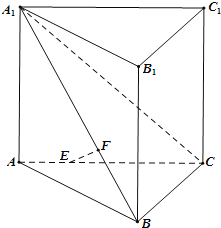
【題目】如圖,在直三棱柱![]() 側棱和底面垂直的棱柱
側棱和底面垂直的棱柱![]() 中,平面
中,平面![]() 側面
側面![]() ,
,![]() ,線段AC、
,線段AC、![]() 上分別有一點E、F且滿足
上分別有一點E、F且滿足![]() ,
,![]() .
.
![]() 求證:
求證:![]() ;
;
![]() 求點E到直線
求點E到直線![]() 的距離;
的距離;
![]() 求二面角
求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從參加高三模擬考試的學生中隨機抽取60名學生,將其數學成績(均為整數)分成六組[90,100),[100,110),…,[140,150]后得到如下部分頻率分布直方圖,觀察圖形的信息,回答下列問題:
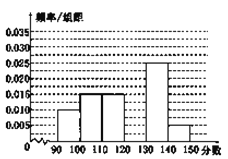
(1)求分數在[120,130)內的頻率;
(2)估計本次考試的中位數;
(3)用分層抽樣的方法在分數段為[110,130)的學生中抽取一個容量為6的樣本,將該樣本看成一個總體,從中任取2人,求至多有1人在分數段[120,130)內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量![]() (噸)與相應的生產能耗
(噸)與相應的生產能耗![]() (噸標準煤)的幾組對照數據
(噸標準煤)的幾組對照數據
|
|
|
|
|
|
|
|
|
|
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)已知該廠技改前100噸甲產品的生產能耗為90噸標準煤.試根據(2)求出的線性同歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?(參考數值![]() )
)
(附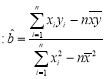 ,
,![]() ,其中
,其中![]() ,
,![]() 為樣本均值)
為樣本均值)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為非空實數集(至少有兩個元素),若對任意
為非空實數集(至少有兩個元素),若對任意![]() ,都有
,都有![]() ,且
,且![]() ,則稱
,則稱![]() 為封閉集,則下列四個判斷:
為封閉集,則下列四個判斷:
①集合![]() 為封閉集,則
為封閉集,則![]() 為無限集; ②集合
為無限集; ②集合![]() 為封閉集;
為封閉集;
③若集合![]() 為封閉集,則
為封閉集,則![]() 為封閉集; ④若
為封閉集; ④若![]() 為封閉集,則一定有
為封閉集,則一定有![]() ;,
;,
其中正確的命題個數有( ).
A.4個B.3個C.2個D.1個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com