Question

若隨機事件A、B互斥，A、B發生的概率均不等于0，且分別為P（A）=2-a，P（B）=3a-4，則實數a的取值范圍為    ．

Answer 1

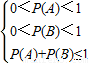
【答案】分析：由隨機事件A、B互斥，A、B發生的概率均不等于0，且分別為P（A）=2-a，P（B）=3a-4，知，由此能求出實數a的取值范圍．
解答：解：∵隨機事件A、B互斥，A、B發生的概率均不等于0，
且分別為P（A）=2-a，P（B）=3a-4，
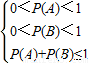
∴，即，
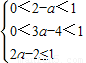
解得．
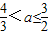
故答案為：（]．
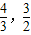
點評：本題考查互斥事件的概率的應用，是基礎題．解題時要認真審題，仔細解答．