
分析 設z=a+bi,(a,b∈R),代入|z|=1+3i-z,利用復數相等的條件列式求得a,b的值,再由復數代數形式的乘除運算化簡得答案.
解答 解:設z=a+bi,(a,b∈R),
而|z|=1+3i-z,即$\sqrt{{a}^{2}+{b}^{2}}-1-3i+a+bi=0$,
則$\left\{\begin{array}{l}{\sqrt{{a}^{2}+{b}^{2}}+a-1=0}\\{b-3=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-4}\\{b=3}\end{array}\right.$,∴z=-4+3i.
∴$\frac{3+4i}{z}=\frac{3+4i}{-4+3i}=\frac{(3+4i)(-4-3i)}{(-4+3i)(-4-3i)}$=$\frac{-25i}{25}=-i$.
點評 本題考查復數代數形式的乘除運算,考查了復數相等的條件,是基礎題.


 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $(\frac{π}{5},0)$ | B. | $(\frac{2π}{5},0)$ | C. | $(\frac{3π}{5},0)$ | D. | $(\frac{4π}{5},0)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{9}$ | B. | $\frac{5π}{18}$ | C. | $\frac{7π}{18}$ | D. | $\frac{11π}{18}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
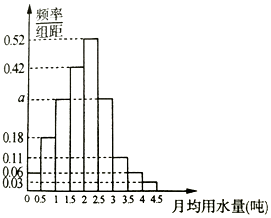 我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準x(噸),一位居民的月用水量不超過x的部分按平價收費,超過x的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5)分成9組,制成了如圖所示的頻率分布直方圖.
我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準x(噸),一位居民的月用水量不超過x的部分按平價收費,超過x的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5)分成9組,制成了如圖所示的頻率分布直方圖.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (5,0),(-5,0) | B. | (0,5),(0,-5) | C. | (0,12),(0,-12) | D. | (12,0),(-12,0) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖所示,某幼兒園有一個游樂場ABCD,其中AB=50米,BC=40米,由于幼兒園招生規模增大,需將該游樂場擴大成矩形區域EFGH,要求A、B、C、D四個點分別在矩形EFGH的四條邊(不含頂點)上.設∠BAE=θ(弧度),EF的長為y米.
如圖所示,某幼兒園有一個游樂場ABCD,其中AB=50米,BC=40米,由于幼兒園招生規模增大,需將該游樂場擴大成矩形區域EFGH,要求A、B、C、D四個點分別在矩形EFGH的四條邊(不含頂點)上.設∠BAE=θ(弧度),EF的長為y米.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com