
分析 設F(c,0),P(m,n),(m<0),設PF的中點為M(0,b),即有m=-c,n=2b,將中點M的坐標代入雙曲線方程,求出a與b的關系,即可求出雙曲線C的漸近線方程.
解答 解:設F(c,0),P(m,n),(m<0),
設PF的中點為M(0,b),
即有m=-c,n=2b,
將點(-c,2b)代入雙曲線方程可得,
$\frac{{c}^{2}}{{a}^{2}}$-$\frac{4{b}^{2}}{{b}^{2}}$=1,
又c2=a2+b2,
∴$\frac{{b}^{2}}{{a}^{2}}$=4,
∴$\frac{b}{a}$=2,
∴雙曲線C的漸近線方程為y=±2x,
故答案為:y=±2x
點評 本題考查雙曲線的方程和性質,主要考查雙曲線的漸近線方程的求法,同時考查中點坐標公式的運用,屬于中檔題.


 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
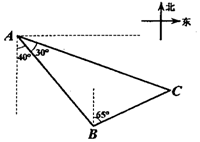 如圖所示,一艘海輪從A處出發,以每小時40海里的速度沿南偏東40°方向直線航行,30分鐘后到達B處,在C處有一座燈塔,海輪在A處觀察燈塔,其方向是南偏東70°,在B處觀察燈塔,其方向是北偏東65°,那么B、C兩點間的距離是10$\sqrt{2}$海里.
如圖所示,一艘海輪從A處出發,以每小時40海里的速度沿南偏東40°方向直線航行,30分鐘后到達B處,在C處有一座燈塔,海輪在A處觀察燈塔,其方向是南偏東70°,在B處觀察燈塔,其方向是北偏東65°,那么B、C兩點間的距離是10$\sqrt{2}$海里.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 24 | B. | 16 | C. | 12 | D. | 8 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com