
分析 設出甲、乙到達的時刻,列出所有基本事件的約束條件同時列出這兩艘船中至少有一艘在停靠泊位時必須等待約束條件,利用線性規劃作出平面區域,利用幾何概型概率公式求出概率
解答 解:設甲到達的時刻為x,乙到達的時刻為y則所有的基本事件構成的區域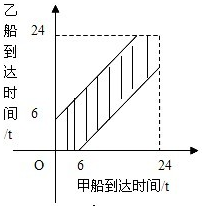
Ω滿足0≤x≤24且0≤y≤24,
這兩艘船中至少有一艘在停靠泊位時必須等待包含的基本事件構成的區域
A滿足0≤x≤24且0≤y≤24且|x-y|≤6,作出對應的平面區域如圖:
這兩艘船中至少有一艘在停靠泊位時必須等待的概率P(A)=$\frac{{S}_{陰影部分}}{{S}_{Ω}}=1-\frac{18×18}{24×24}=\frac{7}{16}$;
故答案為:$\frac{7}{16}$.
點評 本題考查利用線性規劃作出事件對應的平面區域,再利用幾何概型概率公式求出事件的概率.


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (2,+∞) | B. | [2,+∞) | C. | (-∞,2) | D. | (-∞,2] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (3,4) | B. | (-∞,3)∪(4,+∞) | C. | (4,+∞) | D. | (-∞,3) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
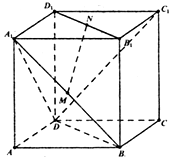 如圖,在正方體ABCD-A1B1C1D1中,點M、N分別是面對角線A1B與B1D1的中點,設$\overrightarrow{DA}$=$\overrightarrow a$,$\overrightarrow{DC}$=$\overrightarrow b$,$\overrightarrow{D{D_1}}$=$\overrightarrow c$.
如圖,在正方體ABCD-A1B1C1D1中,點M、N分別是面對角線A1B與B1D1的中點,設$\overrightarrow{DA}$=$\overrightarrow a$,$\overrightarrow{DC}$=$\overrightarrow b$,$\overrightarrow{D{D_1}}$=$\overrightarrow c$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
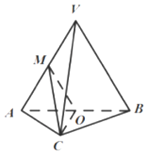 如圖,在三棱錐V-ABC中,平面VAB⊥平面ABC,三角形VAB為等邊三角形,AC⊥BC且 AC=BC=$\sqrt{2}$,O、M分別為AB和VA的中點.
如圖,在三棱錐V-ABC中,平面VAB⊥平面ABC,三角形VAB為等邊三角形,AC⊥BC且 AC=BC=$\sqrt{2}$,O、M分別為AB和VA的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 在等腰梯形ABCD中,已知AB∥DC,∠ABC=60°,BC=$\frac{1}{2}$AB=2,動點E和F分別在線段BC和DC上,且$\overrightarrow{BE}$=λ$\overrightarrow{BC}$,$\overrightarrow{DF}$=$\frac{1}{2λ}$$\overrightarrow{DC}$,則$\overrightarrow{AE}$•$\overrightarrow{BF}$的最小值為4$\sqrt{6}$-13.
在等腰梯形ABCD中,已知AB∥DC,∠ABC=60°,BC=$\frac{1}{2}$AB=2,動點E和F分別在線段BC和DC上,且$\overrightarrow{BE}$=λ$\overrightarrow{BC}$,$\overrightarrow{DF}$=$\frac{1}{2λ}$$\overrightarrow{DC}$,則$\overrightarrow{AE}$•$\overrightarrow{BF}$的最小值為4$\sqrt{6}$-13.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com