
【題目】已知正四棱錐![]() 的所有棱長都相等,
的所有棱長都相等,![]() 是
是![]() 的中點,則
的中點,則![]() ,
,![]() 所成角的正弦值為( )
所成角的正弦值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根據異面直線所成角的定義可得分別取SC,DC,AD邊的中點F,G,H易得EF∥HA,EF=HA,故四邊形AEFH為平行四邊形,所以AE∥DF,又根據中點的性質可得FG∥SD從而將異面直線轉化為了相交直線,即∠HFG或其補角即為異面直線AE、SD所成的角,然后再利用余弦定理,求∠HFG的余弦值即可.
由于正四棱錐S﹣ABCD的側棱長與底面邊長都相等,故不妨設棱長為a.
取SC的中點F,連接EF,則EF∥BC,EF=![]() BC,
BC,
取AD的中點H連接HF則可得EF∥HA,EF=HA,
故四邊形AEFH為平行四邊形,所以AE∥HF.
再取DC中點G,連接HG,則FG∥SD,
所以∠HFG或其補角即為異面直線AE、SD所成的角.
∵HF=AE=![]() a,FG=
a,FG=![]() a,HG=
a,HG=![]() =
=![]() A,
A,
∴cos∠HFG![]() =
=![]() >0.
>0.
即AE、SD所成的角的正弦值為![]() .
.
故選:C.


科目:高中數學 來源: 題型:
【題目】有一隧道內設雙行線公路,其截面由一長方形和一拋物線構成,如圖所示.為保證安全,要求行駛車輛頂部(設為平頂)與隧道頂部在豎直方向上高度之差至少要有![]() 米.若行車道總寬度
米.若行車道總寬度![]() 為
為![]() 米.
米.
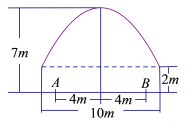
(1)計算車輛通過隧道時的限制高度;
(2)現有一輛載重汽車寬![]() 米,高
米,高![]() 米,試判斷該車能否安全通過隧道?
米,試判斷該車能否安全通過隧道?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1:y=cosx,C2:y=sin(2x+ ![]() ),則下面結論正確的是( )
),則下面結論正確的是( )
A.把C1上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移 ![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
B.把C1上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向左平移 ![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
C.把C1上各點的橫坐標縮短到原來的 ![]() 倍,縱坐標不變,再把得到的曲線向右平移
倍,縱坐標不變,再把得到的曲線向右平移 ![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
D.把C1上各點的橫坐標縮短到原來的 ![]() 倍,縱坐標不變,再把得到的曲線向右平移
倍,縱坐標不變,再把得到的曲線向右平移 ![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐S-ABCD中,底面ABCD是邊長為1的正方形,SD![]() 底面ABCD,SD=2,其中
底面ABCD,SD=2,其中![]() 分別是
分別是![]() 的中點,
的中點,![]() 是
是![]() 上的一個動點.
上的一個動點.
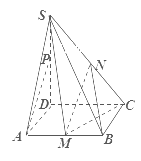
(1)當點![]() 落在什么位置時,
落在什么位置時,![]() ∥平面
∥平面![]() ,證明你的結論;
,證明你的結論;
(2)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,橢圓![]() 的離心率為
的離心率為![]() ,過橢圓右焦點
,過橢圓右焦點![]() 作兩條互相垂直的弦
作兩條互相垂直的弦![]() 與
與![]() .當直線
.當直線![]() 斜率為0時,
斜率為0時,![]() .
.
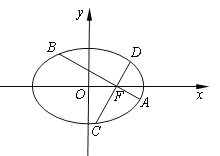
(1)求橢圓的方程;
(2)求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|x<2},B={x|3﹣2x>0},則( )
A.A∩B={x|x< ![]() }
}
B.A∩B=?
C.A∪B={x|x< ![]() }
}
D.AUB=R
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,側面PAD為等邊三角形且垂直于底面ABCD,AB=BC= ![]() AD,∠BAD=∠ABC=90°,E是PD的中點.
AD,∠BAD=∠ABC=90°,E是PD的中點.
(Ⅰ)證明:直線CE∥平面PAB;
(Ⅱ)點M在棱PC 上,且直線BM與底面ABCD所成角為45°,求二面角M﹣AB﹣D的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com