【題目】已知函數
，（ 
）滿足：①
；②
.
（1）求
的值；
（2）若對任意的實數
，都有
成立，求實數
的取值范圍.
【答案】(1)a＝1，c＝2；(2) 
.
【解析】試題分析：（1）根據條件代入二次函數的解析式，求出
的值；（2）轉化為二次函數求最小值小于等于零恒成立，或利用分離參數的方法求m的取值范圍.
試題解析：(1)∵f(1)＝a＋2＋c＝5，∴c＝3－a.①
又∵6＜f(2)＜11，即6＜4a＋c＋4＜11，②
將①式代入②式，得
又∵a、c∈N*，∴a＝1，c＝2.
(2)由(1)知f(x)＝x2＋2x＋2.
法一：設g(x)＝f(x)－2mx＝x2＋2(1－m)x＋2.
當
，即
， 
，故只需
，
解得
，又∵
，故無解.
當
，即
時， 
，故只需
，解得
，
又
，∴
.
綜上可知， 
的取值范圍是
.
法二：∵
，∴不等式
恒成立
在
上恒成立，
易知
，故只需
即可，解得
.
小學教材完全解讀系列答案科目：高中數學 來源： 題型：
【題目】（1）已知橢圓方程為
，點
．
i．若關于原點對稱的兩點
記直線
的斜率分別為
，試計算
的值；
ii．若關于原點對稱的兩點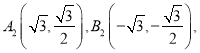
記直線
的斜率分別為
，試計算
的值；
（2）根據上題結論探究：若
是橢圓
上關于原點對稱的兩點，點
是橢圓上任意一點，且直線
的斜率都存在，并分別記為
，試猜想
的值，并加以證明．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分）已知橢圓
：
與拋物線
：
有相同焦點
．
（Ⅰ）求橢圓的標準方程；
（Ⅱ）已知直線
過橢圓
的另一焦點
，且與拋物線
相切于第一象限的點
，設平行
的直線
交橢圓于
兩點，當△
面積最大時，求直線的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓的方程為
＋
＝1(a>b>0)，右焦點為F(c，0)(c>0)，方程ax2＋bx－c＝0的兩實根分別為x1，x2，則P(x1，x2)( )
A．必在圓x2＋y2＝2內
B．必在圓x2＋y2＝2外
C．必在圓x2＋y2＝1外
D．必在圓x2＋y2＝1與圓x2＋y2＝2形成的圓環之間
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x）的圖象如圖所示，曲線BCD為拋物線的一部分．
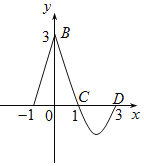
（Ⅰ）求f（x）解析式；
（Ⅱ）若f（x）=1，求x的值；
（Ⅲ）若f（x）＞f（2-x），求x的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
已知在直角坐標系中，曲線
的參數方程為
（
為參數），現以原點為極點，
軸的正半軸為極軸建立極坐標系，直線
的極坐標方程為
．
（1）求曲線
的普通方程和直線
的直角坐標方程；
（2）在曲線
上是否存在一點
，使點
到直線
的距離最小？若存在，求出距離的最小值及點
的直角坐標；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝ax3－
x2＋1(xR)，其中a＞0．
(1)若a＝1，求曲線y＝f(x)在點(2，f(2))處的切線方程；
(2)若在區間
上，f(x)＞0恒成立，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝loga
(其中a>0，且a≠1)．
(1)求函數f(x)的定義域；
(2)判斷函數f(x)的奇偶性并給出證明；
(3)若x∈
時，函數f(x)的值域是[0,1]，求實數a的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
