
分析 (1)由方程g(x)=0有兩個不同的非零實根x1,x2,可得$\frac{a}{b}$>1,結合韋達定理可得x1+x2<-2;
(2)若實數(shù)λ滿足等式f(x1)+f(x2)+3a-λb=0,則λ=$\frac{2a}{b}$ln$\frac{2a}{b}$+$\frac{a}{b}$,進而可得λ的取值范圍.
解答 (本題12分)
證明:(1)由方程g(x)=bx2+2ax+b=0有兩個不同的非零實根,
得△=4a2-4b2>0,
因此a>b>0,
所以$\frac{a}{b}$>1;
所以x1+x2=$-\frac{2a}{b}$<-2;
解:(2)由(1)知x1x2=1,
f(x1)+f(x2)+3a
=aln[x12x22+(x12+x22)+1]+b(x1+x2)+3a
=aln[(x12+x22)+2]+b(x1+x2)+3a
=aln[(x1+x2)2]+b(x1+x2)+3a
=2aln$\frac{2a}{b}$+a,
由f(x1)+f(x2)+3a-λb=0得λ=$\frac{2a}{b}$ln$\frac{2a}{b}$+$\frac{a}{b}$,
設t=$\frac{2a}{b}$>2,則λ=tlnt+$\frac{t}{2}$是增函數(shù).
因此λ>2ln2+1
點評 本題考查的知識點是方程根的存在性質(zhì)及個數(shù)判斷,函數(shù)的單調(diào)性,難度中檔.


科目:高中數(shù)學 來源: 題型:選擇題
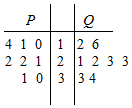 從某工廠生產(chǎn)的P,Q兩種型號的玻璃種分別隨機抽取8個樣品進行檢查,對其硬度系數(shù)進行統(tǒng)計,統(tǒng)計數(shù)據(jù)用莖葉圖表示(如圖所示),則P組數(shù)據(jù)的眾數(shù)和Q組數(shù)據(jù)的中位數(shù)分別為( )
從某工廠生產(chǎn)的P,Q兩種型號的玻璃種分別隨機抽取8個樣品進行檢查,對其硬度系數(shù)進行統(tǒng)計,統(tǒng)計數(shù)據(jù)用莖葉圖表示(如圖所示),則P組數(shù)據(jù)的眾數(shù)和Q組數(shù)據(jù)的中位數(shù)分別為( )| A. | 22和22.5 | B. | 21.5和23 | C. | 22和22 | D. | 21.5和22.5 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,10) |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
 如圖,四棱錐D-ABCO的底面是直角梯形,已知OC∥AB,AB⊥BC,OA=OB,OD⊥DA,AB=2OC,OC=OD=BC=DA=1,DB=$\sqrt{3}$.
如圖,四棱錐D-ABCO的底面是直角梯形,已知OC∥AB,AB⊥BC,OA=OB,OD⊥DA,AB=2OC,OC=OD=BC=DA=1,DB=$\sqrt{3}$.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com