
【題目】已知某工廠每天固定成本是4萬元,每生產(chǎn)一件產(chǎn)品成本增加100元,工廠每件產(chǎn)品的出廠價(jià)定為![]() 元時(shí),生產(chǎn)
元時(shí),生產(chǎn)![]() 件產(chǎn)品的銷售收入是
件產(chǎn)品的銷售收入是![]() (元),
(元),![]() 為每天生產(chǎn)
為每天生產(chǎn)![]() 件產(chǎn)品的平均利潤(平均利潤=總利潤/總產(chǎn)量).銷售商從工廠每件
件產(chǎn)品的平均利潤(平均利潤=總利潤/總產(chǎn)量).銷售商從工廠每件![]() 元進(jìn)貨后又以每件
元進(jìn)貨后又以每件![]() 元銷售,
元銷售, ![]() ,其中
,其中![]() 為最高限價(jià)
為最高限價(jià)![]() ,
, ![]() 為銷售樂觀系數(shù),據(jù)市場調(diào)查,
為銷售樂觀系數(shù),據(jù)市場調(diào)查, ![]() 是由當(dāng)
是由當(dāng)![]() 是
是![]() ,
, ![]() 的比例中項(xiàng)時(shí)來確定.
的比例中項(xiàng)時(shí)來確定.
(1)每天生產(chǎn)量![]() 為多少時(shí),平均利潤
為多少時(shí),平均利潤![]() 取得最大值?并求
取得最大值?并求![]() 的最大值;
的最大值;
(2)求樂觀系數(shù)![]() 的值;
的值;
(3)若![]() ,當(dāng)廠家平均利潤最大時(shí),求
,當(dāng)廠家平均利潤最大時(shí),求![]() 與
與![]() 的值.
的值.
【答案】(1)400,200;(2)![]() ;(3)
;(3)![]() ,
, ![]() .
.
【解析】試題分析:(1)先求出總利潤=![]() ,依據(jù)(平均利潤=總利潤/總產(chǎn)量)可得
,依據(jù)(平均利潤=總利潤/總產(chǎn)量)可得![]() ,利用均值不等式得最大利潤;(2)由已知得
,利用均值不等式得最大利潤;(2)由已知得![]() ,結(jié)合比例中項(xiàng)的概念可得
,結(jié)合比例中項(xiàng)的概念可得![]() ,兩邊同時(shí)除以
,兩邊同時(shí)除以![]() 將等式化為
將等式化為![]() 的方程,解出方程即可;(3)利用
的方程,解出方程即可;(3)利用![]() 平均成本
平均成本![]()
![]() 平均利潤
平均利潤![]() ,結(jié)合廠家平均利潤最大時(shí)(由(1)的結(jié)果)可得
,結(jié)合廠家平均利潤最大時(shí)(由(1)的結(jié)果)可得![]() 的值,利用
的值,利用![]() 可得
可得![]() 的值.
的值.
試題解析:(1)依題意總利潤=![]() ,
,
=![]() ,
,
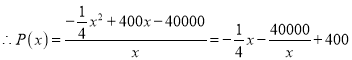 ,
,
![]() 此時(shí)
此時(shí)![]() ,
, ![]() ,
,
即,每天生產(chǎn)量為400件時(shí),平均利潤最大,最大值為200元 .
(2)由![]() 得
得![]() ,
, ![]() 是
是![]() 的比例中項(xiàng),
的比例中項(xiàng),
![]() ,
,
兩邊除以![]() 得
得![]() ,
,
![]() 解得
解得![]() .
.
(3)廠家平均利潤最大, ![]() 元,
元,
每件產(chǎn)品的毛利為![]() ,
, ![]() ,
,
![]() 元,
元, ![]() (元),
(元),![]() 元.
元.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,點(diǎn)E為棱PC的中點(diǎn). 
(1)證明:BE∥平面ADP;
(2)求直線BE與平面PDB所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,底面ABCD為矩形,PA⊥平面ABCD,E為PD的中點(diǎn).
(1)證明:PB∥平面AEC;
(2)設(shè)AP=1,AD= ![]() ,三棱錐P﹣ABD的體積V=
,三棱錐P﹣ABD的體積V= ![]() ,求A到平面PBC的距離.
,求A到平面PBC的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線l1:y=kx﹣1與雙曲線x2﹣y2=1的左支交于A,B兩點(diǎn).
(1)求斜率k的取值范圍;
(2)若直線l2經(jīng)過點(diǎn)P(﹣2,0)及線段AB的中點(diǎn)Q且l2在y軸上截距為﹣16,求直線l1的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 分別是橢圓
分別是橢圓![]() 的長軸與短軸的一個端點(diǎn),
的長軸與短軸的一個端點(diǎn), ![]() 是橢圓的左、右焦點(diǎn),以
是橢圓的左、右焦點(diǎn),以![]() 點(diǎn)為圓心、3為半徑的圓與以
點(diǎn)為圓心、3為半徑的圓與以![]() 點(diǎn)為圓心、1為半徑的圓的交點(diǎn)在橢圓
點(diǎn)為圓心、1為半徑的圓的交點(diǎn)在橢圓![]() 上,且
上,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() 為橢圓
為橢圓![]() 上一點(diǎn),直線
上一點(diǎn),直線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,直線
,直線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,以橢圓的一個短軸端點(diǎn)及兩個焦點(diǎn)構(gòu)成的三角形的面積為
,以橢圓的一個短軸端點(diǎn)及兩個焦點(diǎn)構(gòu)成的三角形的面積為![]() ,圓C方程為
,圓C方程為![]() .
.
(1)求橢圓及圓C的方程;
(2)過原點(diǎn)O作直線l與圓C交于A,B兩點(diǎn),若![]() ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 滿足
滿足![]() ,
, ![]()
![]() .
.
(1)求證:數(shù)列![]() 為等差數(shù)列;
為等差數(shù)列;
(2)求數(shù)列![]() 的前
的前![]() 項(xiàng)和
項(xiàng)和![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,以O(shè)x軸為始邊作兩個銳角α,β,它們的終邊分別交單位圓于A,B兩點(diǎn).已知A,B兩點(diǎn)的橫坐標(biāo)分別是 ![]() ,
, ![]() .
. 
(1)求tan(α+β)的值;
(2)求α+2β的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com