
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,以橢圓的一個短軸端點及兩個焦點構成的三角形的面積為
,以橢圓的一個短軸端點及兩個焦點構成的三角形的面積為![]() ,圓C方程為
,圓C方程為![]() .
.
(1)求橢圓及圓C的方程;
(2)過原點O作直線l與圓C交于A,B兩點,若![]() ,求直線l的方程.
,求直線l的方程.
【答案】(1)橢圓的方程![]() ,圓的方程為
,圓的方程為![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
試題分析:(1)由離心率為![]() 可得
可得![]() ,結合
,結合![]() 得
得![]() ,根據以橢圓的一個短軸端點及兩個焦點為頂點的三角形面積為
,根據以橢圓的一個短軸端點及兩個焦點為頂點的三角形面積為![]() 可得
可得![]() ,從而求的
,從而求的![]() ,得到橢圓和圓的方程;(2)設出直線
,得到橢圓和圓的方程;(2)設出直線![]() 的方程,整理方程組,由判別式求出直線斜率的范圍,韋達定理得到
的方程,整理方程組,由判別式求出直線斜率的范圍,韋達定理得到![]() 坐標的關系,根據向量數量積的坐標表示列出方程,求的斜率
坐標的關系,根據向量數量積的坐標表示列出方程,求的斜率![]() .
.
試題解析:(1)設橢圓的焦距為2c,左、右焦點分別為![]() ,由橢圓的離心率為
,由橢圓的離心率為![]() 可得
可得![]() ,即
,即![]() ,所以
,所以![]()
以橢圓的一個短軸端點及兩個焦點為頂點的三角形的面積為![]() ,即
,即![]() ,
,![]()
所以橢圓的方程![]() ,圓的方程為
,圓的方程為![]()
(2)①當直線![]() 的斜率不存時,直線方程為
的斜率不存時,直線方程為![]() ,與圓C相切,不符合題意
,與圓C相切,不符合題意
②當直線![]() 的斜率存在時,設直線方程
的斜率存在時,設直線方程![]() ,
,
由![]() 可得
可得![]() ,
,
由條件可得![]() ,即
,即![]()
設![]() ,
,![]() ,則
,則![]() ,
,![]()
![]()
而圓心C的坐標為(2,1)則![]()
![]() ,
,
所以![]() ,
,
即![]()
所以![]() 解得
解得![]() 或
或![]()
![]() 或
或![]()


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
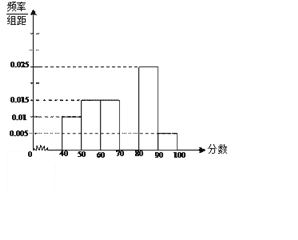
【題目】某校從參加考試的學生中抽出60名學生,將其成績(均為整數)分成六組[40,50),[50,60) ...[90,100]后,畫出如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
(Ⅰ) 求成績落在[70,80)上的頻率,并補全這個頻率分布直方圖;
(Ⅱ) 估計這次考試的及格率(60分及以上為及格)和平均分;
(Ⅲ) 設學生甲、乙的成績屬于區間[40,50),現從成績屬于該區間的學生中任選兩人,求甲、乙中至少有一人被選的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】劉老師是一位經驗豐富的高三理科班班主任,經長期研究,他發現高中理科班的學生的數學成績(總分150分)與理綜成績(物理、化學與生物的綜合,總分300分)具有較強的線性相關性,以下是劉老師隨機選取的八名學生在高考中的數學得分x與理綜得分y(如下表):
學生編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
數學分數x | 52 | 64 | 87 | 96 | 105 | 123 | 132 | 141 |
理綜分數y | 112 | 132 | 177 | 190 | 218 | 239 | 257 | 275 |
參考數據及公式: ![]() .
.
(1)求出y關于x的線性回歸方程;
(2)若小汪高考數學110分,請你預測他理綜得分約為多少分?(精確到整數位);
(3)小金同學的文科一般,語文與英語一起能穩定在215分左右.如果他的目標是在
高考總分沖擊600分,請你幫他估算他的數學與理綜大約分別至少需要拿到多少分?(精確到整數位).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年天貓五一活動結束后,某地區研究人員為了研究該地區在五一活動中消費超過3000元的人群的年齡狀況,隨機在當地消費超過3000元的群眾中抽取了500人作調查,所得概率分布直方圖如圖所示:記年齡在![]() ,
, ![]() ,
, ![]() 對應的小矩形的面積分別是
對應的小矩形的面積分別是![]() ,且
,且![]() .
.
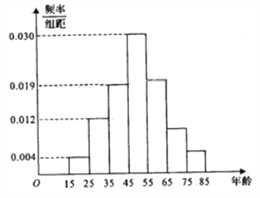
(1)以頻率作為概率,若該地區五一消費超過3000元的有30000人,試估計該地區在五一活動中消費超過3000元且年齡在![]() 的人數;
的人數;
(2)若按照分層抽樣,從年齡在![]() 的人群中共抽取6人,再從這6人中隨機抽取2人作深入調查,求至少有1人的年齡在
的人群中共抽取6人,再從這6人中隨機抽取2人作深入調查,求至少有1人的年齡在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 滿足:對任意
滿足:對任意![]() ,
,![]() ,都有
,都有![]() 成立,且
成立,且![]() 時,
時,![]() .
.
(1)求![]() 的值,并證明:當
的值,并證明:當![]() 時,
時,![]() ;
;
(2)判斷![]() 的單調性并加以證明;
的單調性并加以證明;
(3)若函數![]() 在
在![]() 上遞減,求實數
上遞減,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】衡州市臨棗中學高二某小組隨機調查芙蓉社區160個人,以研究這一社區居民在20:00-22:00時間段的休閑方式與性別的關系,得到下面的數據表:
休閑方式 性別 | 看電視 | 看書 | 合計 |
男 | 20 | 100 | 120 |
女 | 20 | 20 | 40 |
合計 | 40 | 120 | 160 |
下面臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
(Ⅰ)將此樣本的頻率估計為總體的概率,隨機調查3名在該社區的男性,設調查的3人在這一時間段以看書為休閑方式的人數為隨機變量![]() ,求
,求![]() 的分別列和期望;
的分別列和期望;
(Ⅱ)根據以上數據,能否有99%的把握認為“在20:00-22:00時間段的休閑方式與性別有關系”?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,橢圓
,橢圓![]() 的離心率為
的離心率為![]() ,
,![]() 是橢圓
是橢圓![]() 的右焦點,直線
的右焦點,直線![]() 的斜率為
的斜率為![]() ,
,![]() 為坐標原點.
為坐標原點.
(1)求![]() 的方程;
的方程;
(2)設過點![]() 的動直線
的動直線![]() 與
與![]() 相交于
相交于![]() 兩點,問:是否存在直線
兩點,問:是否存在直線![]() ,使以
,使以![]() 為直徑的圓經過原點
為直徑的圓經過原點![]() ,若存在,求出對應直線
,若存在,求出對應直線![]() 的方程,若不存在,請說明理由.
的方程,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com