【題目】如圖，在四棱錐P ABCD中，E是棱PC上一點，且2
，底面ABCD是邊長為2的正方形，△PAD為正三角形，平面ABE與棱PD交于點F，平面PCD與平面PAB交于直線l，且平面PAD⊥平面ABCD.
(1)求證：l∥EF；
(2)求四棱錐P-ABEF的體積．
【答案】（1）見解析； （2）
.
【解析】
(1) 取PD的中點F,連接EF,先證明AB||平面PCD,再證明l∥EF.（2）先證明PF
面
，再求四棱錐P-ABEF的體積．
證明：取PD的中點F,連接EF,
∵底面ABCD是正方形，∴AB∥CD，
因為2
，所以點E是PC的中點，所以PE=EC,
因為DF=PF,所以EF||CD,
因為AB||CD,所以AB||EF,因為
,
所以AB||平面PCD,
又平面PAB與平面PCD交于直線l，
,
∴AB∥l.
∴l∥EF.
（2）由面
面
，交線為
因為CD⊥平面PAD,
面
，
所以EF⊥PF,
因為AF⊥PF,因為AF,EF
面，AF∩EF=F,
所以PF面，
所以
，
所以體積為
課時訓練江蘇人民出版社系列答案科目：高中數學 來源： 題型：
【題目】設函數f（x）=|x+1|+|x﹣4|﹣a．
（1）當a=1時，求函數f（x）的最小值；
（2）若f（x）≥ 
+1對任意的實數x恒成立，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱
中，側棱垂直于底面，
， 
為
的中點，過
的平面與
交于點
．
（1）求證：點為的中點；
（2）四邊形
是什么平面圖形？說明理由，并求其面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】三棱錐P ABC中，PA⊥平面ABC，
Q是BC邊上的一個動點，且直線PQ與面ABC所成角的最大值為
則該三棱錐外接球的表面積為( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，在矩形ABCD中，AB＝3，BC＝4，E，F分別在線段BC，AD上，EF∥AB，將矩形ABEF沿EF折起，記折起后的矩形為MNEF，且平面MNEF⊥平面ECDF.
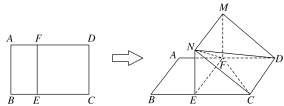
(1)在線段BC是否存在一點E，使得ND⊥FC ，若存在，求出EC的長并證明；
若不存在，請說明理由．
(2)求四面體NEFD體積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】己知
，
分別為橢圓C:
的左、右焦點，點
在橢圓C上．
（1）求
的最小值；
（2）已知直線l：
與橢圓C交于兩點A、B，過點
且平行于直線l的直線交橢圓C于另一點Q，問：四邊形PABQ能否成為平行四邊形？若能，請求出直線l的方程；若不能，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知平面直角坐標系xOy中，圓C的參數方程為 
（θ為參數，r＞0）．以直角坐標系原點O為極點，x軸的正半軸為極軸建立極坐標系，直線l的極坐標方程為 
ρsin（θ+ 
）+1=0．
（1）求圓C的圓心的極坐標；
（2）當圓C與直線l有公共點時，求r的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖的程序圖的算法思路中是一種古老而有效的算法﹣﹣輾轉相除法，執行改程序框圖，若輸入的m，n的值分別為30，42，則輸出的m=（ ）
A.0
B.2
C.3
D.6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
