
分析 列出滿足條件約束條件,畫出滿足條件的可行域,進而可得答案.
解答 解:由題意,要使函數f(x)=x2+ax+b在區間[-$\frac{1}{2}$,0]有零點,
只要$f(-\frac{1}{2})•f(0)≤0$,或$\left\{\begin{array}{l}f(0)=1+b≥0\\ f(-\frac{1}{2})=\frac{1}{4}-\frac{1}{2}a+b≥0\\-\frac{1}{2}<-\frac{a}{2}<0\\△={a}^{2}-4b>0\end{array}\right.$,
其對應的平面區域如下圖所示:

則當a=1,b=-1時,a-2b取最大值3,
當a=0,b=0時,a-2b取最小值0,
所以a-2b的取值范圍為[0,3];
故答案為:[0,3].
點評 本題考查了函數零點的分布,線性規劃,關鍵是結合二次函數圖象等價得到不等式組.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
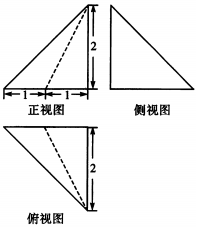
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | $f(x)=2sin(2x-\frac{π}{6})$ | B. | $f(x)=2sin(x+\frac{π}{6})$ | C. | $f(x)=2sin(2x+\frac{π}{3})$ | D. | $f(x)=2sin(2x+\frac{π}{6})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
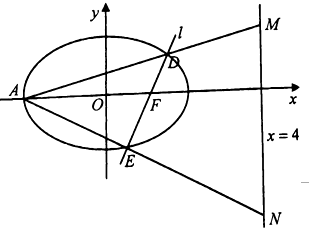 已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦點為F,短軸長為2$\sqrt{3}$,點P為橢圓C上一點,且點P到點F的最遠距離是最近距離的3倍.
已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦點為F,短軸長為2$\sqrt{3}$,點P為橢圓C上一點,且點P到點F的最遠距離是最近距離的3倍.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com