
分析 在二項展開式的通項公式:Tr+1=${C}_{5}^{r}$•x15-3r•(-1)r•x-2r=(-1)r•${C}_{5}^{r}$•x15-5r,令x的冪指數等于0,即15-5r=0,求出r的值,即常數項-${C}_{5}^{r}$=-10.
解答 解:由題意可知:${({x^3}-\frac{1}{x^2})^5}$的二項展開式的通項公式為:Tr+1=${C}_{5}^{r}$•x15-3r•(-1)r•x-2r=(-1)r•${C}_{5}^{r}$•x15-5r,
令15-5r=0,解得r=3,
故展開式中的常數項為-${C}_{5}^{r}$=-10,
故答案為:-10.
點評 本題主要考查二項式定理的應用,二項展開式的通項公式,求展開式中某項的系數,屬于基礎題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
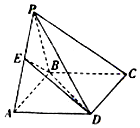 如圖,四棱錐P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中點,且PA=PB=AB=2,BC=$\sqrt{2}$.
如圖,四棱錐P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中點,且PA=PB=AB=2,BC=$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
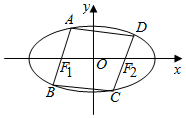 如圖所示,橢圓C:$\frac{{x}^{2}}{4}$+y2=1,左右焦點分別記作F1,F2,過F1,F2分別作直線l1,l2交橢圓AB,CD,且l1∥l2.
如圖所示,橢圓C:$\frac{{x}^{2}}{4}$+y2=1,左右焦點分別記作F1,F2,過F1,F2分別作直線l1,l2交橢圓AB,CD,且l1∥l2.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com