
過拋物線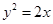 的焦點
的焦點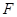 作直線
作直線 交拋物線于
交拋物線于 兩點,若
兩點,若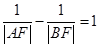 ,則直線
,則直線 的傾斜角
的傾斜角 。
。
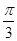 或
或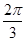
解析試題分析:由題意可得:F(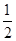 ,0)設A(x1,y1),B(x2,y2).因為過拋物線y2=2x的焦點F作直線l交拋物線于A、B兩點,所以|AF|=
,0)設A(x1,y1),B(x2,y2).因為過拋物線y2=2x的焦點F作直線l交拋物線于A、B兩點,所以|AF|=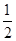 +x1,|BF|=
+x1,|BF|=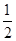 +x2.又因為
+x2.又因為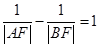 ,所以|AF|<|BF|,即x1<x2,并且直線l的斜率存在.設直線l的方程為y=k(x-
,所以|AF|<|BF|,即x1<x2,并且直線l的斜率存在.設直線l的方程為y=k(x-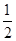 ),聯立直線與拋物線的方程可得:k2x2-(k2+2)x+
),聯立直線與拋物線的方程可得:k2x2-(k2+2)x+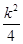 =0,所以x1+x2=
=0,所以x1+x2=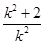 ,x1x2=
,x1x2=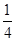 .因為
.因為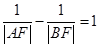 ,所以整理可得
,所以整理可得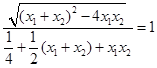 ,即整理可得k4-2k2-3=0,所以解得k2=3.因為0<θ≤
,即整理可得k4-2k2-3=0,所以解得k2=3.因為0<θ≤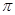 ,所以k=
,所以k=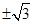 ,即θ=
,即θ=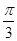 或
或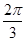
考點:本題考查了直線的傾斜角;拋物線的簡單性質.
點評:解決此類問題的關鍵是熟練掌握拋物線的定義,以及掌握直線與拋物線位置關系,并且結合準確的運算也是解決此類問題的一個重要方面


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:高中數學 來源: 題型:填空題
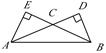
如圖,在△ABC中,∠CAB=∠CBA=30°,AC、BC邊上的高分別為BD、AE,則以A、B為焦點,且過D、E的橢圓與雙曲線的離心率分別為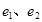 ,則
,則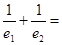 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com