
【題目】2017年5月13日第30屆大連國際馬拉松賽舉行,某單位的10名跑友報名參加了半程馬拉松、10公里健身跑、迷你馬拉松3個項目(每人只報一項),報名情況如下:
項目 | 半程馬拉松 | 10公里健身跑 | 迷你馬拉松 |
人數 | 2 | 3 | 5 |
(其中:半程馬拉松![]() 公里,迷你馬拉松
公里,迷你馬拉松![]() 公里)
公里)
(1)從10人中選出2人,求選出的兩人賽程距離之差大于10公里的概率;
(2)從10人中選出2人,設![]() 為選出的兩人賽程距離之和,求隨機變量
為選出的兩人賽程距離之和,求隨機變量![]() 的分布列.
的分布列.
 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:高中數學 來源: 題型:
【題目】在長方體![]() 中,
中,![]() 分別是
分別是![]() 的中點,
的中點,![]() ,過
,過![]() 三點的的平面截去長方體的一個角后.得到如圖所示的幾何體
三點的的平面截去長方體的一個角后.得到如圖所示的幾何體![]() ,且這個幾何體的體積為
,且這個幾何體的體積為![]() .
.
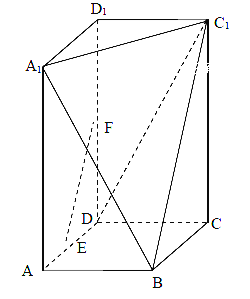
(1)求證:![]() 平面
平面![]() ;
;
(2)求![]() 的長;
的長;
(3)在線段![]() 上是否存在點
上是否存在點![]() ,使直線
,使直線![]() 與
與![]() 垂直,如果存在,求線段
垂直,如果存在,求線段![]() 的長,如果不存在,請說明理由.
的長,如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產的新產品必須先靠廣告打開銷路,該產品廣告效應y(單位:元)是產品的銷售額與廣告費x(單位:元)之間的差,如果銷售額與廣告費x的算術平方根成正比,根據對市場的抽樣調查,每付出100元的廣告費,所得銷售額是1000元. (Ⅰ)求出廣告效應y與廣告費x之間的函數關系式;
(Ⅱ)該企業投入多少廣告費才能獲得最大的廣告效應?是不是廣告費投入越多越好?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知下列命題:
①若![]() ,則“
,則“![]() ”是“
”是“![]() ”成立的充分不必要條件;
”成立的充分不必要條件;
②若橢圓![]() 的兩個焦點為
的兩個焦點為![]() ,且弦
,且弦![]() 過點
過點![]() ,則
,則![]() 的周長為16;
的周長為16;
③若命題“![]() ”與命題“
”與命題“![]() 或
或![]() ”都是真命題,則命題
”都是真命題,則命題![]() 一定是真命題;
一定是真命題;
④若命題![]() :
: ![]() ,則
,則![]() :
: ![]()
其中為真命題的是__________(填序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】王明參加某衛視的闖關活動,該活動共3關.設他通過第一關的概率為0.8,通過第二、第三關的概率分別為p,q,其中![]() ,并且是否通過不同關卡相互獨立.記ξ為他通過的關卡數,其分布列為:
,并且是否通過不同關卡相互獨立.記ξ為他通過的關卡數,其分布列為:
ξ | 0 | 1 | 2 | 3 |
P | 0.048 | a | b | 0.192 |
(Ⅰ)求王明至少通過1個關卡的概率;
(Ⅱ)求p,q的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為評估設備![]() 生產某種零件的性能,從設備
生產某種零件的性能,從設備![]() 生產零件的流水線上隨機抽取100件零件作為樣本,測量其直徑后,整理得到下表:
生產零件的流水線上隨機抽取100件零件作為樣本,測量其直徑后,整理得到下表:
直徑/ | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合計 |
件數 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
經計算,樣本的平均值![]() ,標準差
,標準差![]() ,以頻率值作為概率的估計值.
,以頻率值作為概率的估計值.
(1)為評判一臺設備的性能,從該設備加工的零件中任意抽取一件,記其直徑為![]() ,并根據以下不等式進行評判(
,并根據以下不等式進行評判(![]() 表示相應事件的概率);
表示相應事件的概率);
①![]() ;
;
②![]() ;
;
③![]()
評判規則為:若同時滿足上述三個不等式,則設備等級為甲;僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部不滿足,則等級為丁,試判斷設備![]() 的性能等級.
的性能等級.
(2)將直徑小于等于![]() 或直徑大于
或直徑大于![]() 的零件認為是次品.
的零件認為是次品.
①從設備![]() 的生產流水線上隨意抽取2件零件,計算其中次品個數
的生產流水線上隨意抽取2件零件,計算其中次品個數![]() 的數學期望
的數學期望![]() ;
;
②從樣本中隨意抽取2件零件,計算其中次品個數![]() 的數學期望
的數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com