【答案】
分析:(I)由已知中函數f(x)=(x
2+ax+b)e
3-x(x∈R)的一個極值點是x=3.我們根據函數在某點取得極值的條件,易得f′(3)=0,進而構造方程求出a與b的關系式,分析函數在各個區間上的符號,即可得到答案.
(II)根據g(x)=(a
2+
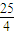
)e
x,利用導數法確定函數的單調性,再根據(1)的結論,我們可以構造一個關于a的不等式,解不等式即可得到答案.
解答:解:(Ⅰ)f′(x)=-e
3-x,(1分)
由f′(3)=0,得-e
3-3=0,即得b=-3-2a,(2分)
則f′(x)=e
3-x=-e
3-x=-(x-3)(x+a+1)e
3-x.
令f′(x)=0,得x
1=3或x
2=-a-1,由于x=3是極值點,∴-a-1≠3,即a≠-4,(4分)
當a<-4時,x
2>3=x
1,則在區間(-∞,3)上,f′(x)<0,
f(x)為減函數;在區間(3,-a-1)上,f′(x)>0,f(x)為增函數;
在區間(-a-1,+∞)上,f′(x)<0,f(x)為減函數. (5分)
當a>-4時,x
2<3=x
1,則在區間(-∞,-a-1)上,f′(x)<0,f(x)為減函數;
在區間(-a-1,3)上,f′(x)>0,f(x)為增函數;在區間(3,+∞)上,f′(x)<0,f(x)為減函數;
(Ⅱ)由(Ⅰ)知,當a>0時,f(x)在區間(0,3)上的單調遞增,在區間(3,4)上單調遞減,由于f(x)連續,那么f(x)在區間上的值域是,而f(0)=-(2a+3)e
3<0,f(4)=(2a+13)e
-1>0,f(3)=a+6,
那么f(x)在區間上的值域是(8分) 又g(x)=)=(a
2+
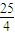
)e
x,
在區間上是增函數,且它在區間上的值域是,.(10分)
由于(a
2+
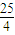
)-(a+6)=a
2-a+

=(a-

)
2≥0,
所以只須僅須(a
2+
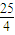
)-(a+6)<1且a>0,解得0<a<

.故a的取值范圍是(0,

) (12分).
點評:本題考查的知識點是函數在某點取得極值的條件,利用導數研究函數的單調性,其中根據已知中的函數的解析式,結合導數公式,求出函數的導函數的解析式,是解答本題的關鍵.

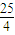 )ex若存在ε1,ε2∈[0,4]使得f(ε1)-g(ε2)<1成立,求a的取值范圍.
)ex若存在ε1,ε2∈[0,4]使得f(ε1)-g(ε2)<1成立,求a的取值范圍.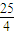 )ex,利用導數法確定函數的單調性,再根據(1)的結論,我們可以構造一個關于a的不等式,解不等式即可得到答案.
)ex,利用導數法確定函數的單調性,再根據(1)的結論,我們可以構造一個關于a的不等式,解不等式即可得到答案.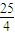 )ex,
)ex,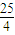 )-(a+6)=a2-a+
)-(a+6)=a2-a+ =(a-
=(a- )2≥0,
)2≥0,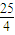 )-(a+6)<1且a>0,解得0<a<
)-(a+6)<1且a>0,解得0<a< .故a的取值范圍是(0,
.故a的取值范圍是(0, ) (12分).
) (12分).
