
【題目】已知正三棱柱![]() 的底面邊長為
的底面邊長為![]() ,
,![]() 為
為![]() 的中點,平面
的中點,平面![]() 與平面
與平面![]() 所成的銳二面角的正切值是
所成的銳二面角的正切值是![]() ,則四棱錐
,則四棱錐![]() 外接球的表面積為________.
外接球的表面積為________.
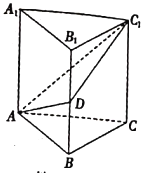
【答案】![]()
【解析】
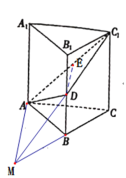
延長C1D與CB的延長線交于點M,連接AM.推導出D也是C1M的中點,AM∥DE,AM⊥平面ACC1A1,可得![]() ;再根據四棱錐A-BC
;再根據四棱錐A-BC![]() 外接球即為正三棱柱ABC-
外接球即為正三棱柱ABC-![]() 的外接球,找到球心位置,根據勾股數求得半徑,即可得到表面積.
的外接球,找到球心位置,根據勾股數求得半徑,即可得到表面積.
如圖,延長C1D與CB的延長線交于點M,連接AM.
∵B1C1∥BC,D為BB1的中點,∴D也是C1M的中點,
又取E是AC1的中點,∴AM∥DE.
∵DE⊥平面ABB1A1,∴AM⊥平面ACC1A1.
∴∠C1AC為平面AC1D與平面ABC所成二面角的平面角.
∴tan∠C1AC![]() ,∴
,∴![]() ,又AC=
,又AC=![]() ,則
,則![]()
又四棱錐A-BC![]() 外接球即為正三棱柱
外接球即為正三棱柱![]() 的外接球,其球心在底面ABC中心正上方的
的外接球,其球心在底面ABC中心正上方的![]() 處,又底面外接圓的半徑為2r=
處,又底面外接圓的半徑為2r=![]() ∴
∴![]() ,
,
∴四棱錐![]() 外接球的表面積為
外接球的表面積為![]() ,
,
故答案為19![]() .
.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的奇函數,當
上的奇函數,當![]() 時,
時,![]() .則下列結論正確的是( ).
.則下列結論正確的是( ).
A.當![]() 時,
時,![]()
B.函數![]() 有五個零點
有五個零點
C.若關于![]() 的方程
的方程![]() 有解,則實數
有解,則實數![]() 的取值范圍是
的取值范圍是![]()
D.對![]() ,
,![]() 恒成立
恒成立
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某社區為了解居民參加體育鍛煉情況,隨機抽取18名男性居民,12名女性居民對他們參加體育鍛煉的情況進行問卷調查.現按參加體育鍛煉的情況將居民分成3類:甲類(不參加體育鍛煉),乙類(參加體育鍛煉,但平均每周參加體育鍛煉的時間不超過5個小時),丙類(參加體育鍛煉,且平均每周參加體育鍛煉的時間超過5個小時),調查結果如下表:
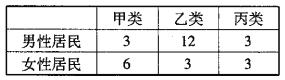
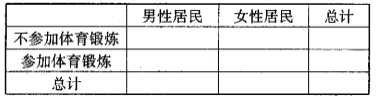
(1)根據表中的統計數據,完成下面列聯表,并判斷是否有![]() 的把握認為參加體育鍛煉與性別有關?
的把握認為參加體育鍛煉與性別有關?
(2)從抽出的女性居民中再隨機抽取3人進一步了解情況,記![]() 為抽取的這3名女性居民中甲類和丙類人數差的絕對值,求
為抽取的這3名女性居民中甲類和丙類人數差的絕對值,求![]() 的數學期望.
的數學期望.
附:![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為研究學生的身體素質與體育鍛煉時間的關系,對該校300名高三學生平均每天體育鍛煉時間進行調查,如表:(平均每天鍛煉的時間單位:分鐘).
平均每天鍛煉的時間/分鐘 |
|
|
|
|
|
|
總人數 | 34 | 51 | 59 | 66 | 65 | 25 |
將學生日均體育鍛煉時間在![]() 的學生評價為“鍛煉達標”.
的學生評價為“鍛煉達標”.
(1)請根據上述表格中的統計數據填寫下面的![]() 列聯表;
列聯表;
鍛煉不達標 | 鍛煉達標 | 合計 | |
男 | |||
女 | 40 | 160 | |
合計 |
(2)通過計算判斷,是否能在犯錯誤的概率不超過0.05的前提下認為“鍛煉達標”與性別有關?
參考公式:![]() ,其中
,其中![]() .
.
臨界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
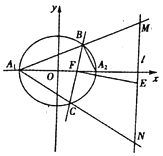
【題目】如圖,已知橢圓![]()
![]() 的長軸
的長軸![]() ,長為4,過橢圓的右焦點
,長為4,過橢圓的右焦點![]() 作斜率為
作斜率為![]() (
(![]() )的直線交橢圓于
)的直線交橢圓于![]() 、
、![]() 兩點,直線
兩點,直線![]() ,
,![]() 的斜率之積為
的斜率之積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() ,直線
,直線![]() ,
,![]() 分別與
分別與![]() 相交于
相交于![]() 、
、![]() 兩點,設
兩點,設![]() 為線段
為線段![]() 的中點,求證:
的中點,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[2019·吉林期末]一個袋中裝有6個大小形狀完全相同的球,球的編號分別為1,2,3,4,5,6.
(1)從袋中隨機抽取兩個球,求取出的球的編號之和為6的概率;
(2)先后有放回地隨機抽取兩個球,兩次取的球的編號分別記為![]() 和
和![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,原點為
,原點為![]() ,橢圓
,橢圓![]() 的動弦
的動弦![]() 過焦點
過焦點![]() 且不垂直于坐標軸,弦
且不垂直于坐標軸,弦![]() 的中點為
的中點為![]() ,過
,過![]() 且垂直于線段
且垂直于線段![]() 的直線交射線
的直線交射線![]() 于點
于點![]() .
.
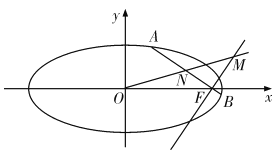
(Ⅰ)證明:點![]() 在定直線上;
在定直線上;
(Ⅱ)當![]() 最大時,求
最大時,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,射線OA、OB分別與x軸正半軸成45°和30°角,過點P(1,0)作直線AB分別交OA、OB于A、B兩點,當AB的中點C恰好落在直線y=![]() x上時,求直線AB的方程.
x上時,求直線AB的方程.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com