
【題目】某社區為了解居民參加體育鍛煉情況,隨機抽取18名男性居民,12名女性居民對他們參加體育鍛煉的情況進行問卷調查.現按參加體育鍛煉的情況將居民分成3類:甲類(不參加體育鍛煉),乙類(參加體育鍛煉,但平均每周參加體育鍛煉的時間不超過5個小時),丙類(參加體育鍛煉,且平均每周參加體育鍛煉的時間超過5個小時),調查結果如下表:
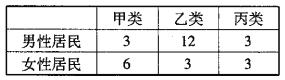
(1)根據表中的統計數據,完成下面列聯表,并判斷是否有![]() 的把握認為參加體育鍛煉與性別有關?
的把握認為參加體育鍛煉與性別有關?
(2)從抽出的女性居民中再隨機抽取3人進一步了解情況,記![]() 為抽取的這3名女性居民中甲類和丙類人數差的絕對值,求
為抽取的這3名女性居民中甲類和丙類人數差的絕對值,求![]() 的數學期望.
的數學期望.
附:![]()
|
|
|
|
|
|
|
|
|
|
 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案 走進文言文系列答案
走進文言文系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,已知AB為圓O的直徑,且![]() ,點D為線段AO的中點,點C為圓O上的一點,且
,點D為線段AO的中點,點C為圓O上的一點,且![]() ,
,![]() 平面ABC,
平面ABC,![]() .
.

(1)求證:![]() 平面PAB.
平面PAB.
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的左、右焦點分別是
的左、右焦點分別是![]() ,
,![]() ,離心率為
,離心率為![]() ,過
,過![]() 且垂直于
且垂直于![]() 軸的直線被橢圓
軸的直線被橢圓![]() 截得的線段長為1.
截得的線段長為1.
(1)求橢圓![]() 的方程;
的方程;
(2)點![]() 是橢圓
是橢圓![]() 上除長軸端點外的任一點,連接
上除長軸端點外的任一點,連接![]() ,
,![]() ,設
,設![]() 的角平分線
的角平分線![]() 交
交![]() 的長軸于點
的長軸于點![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() ,使得
,使得![]() 與橢圓
與橢圓![]() 有且只有一個公共點,設直線
有且只有一個公共點,設直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,若
,若![]() ,證明
,證明![]() 為定值,并求出這個定值.
為定值,并求出這個定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖在直角梯形ABCD中,AB//CD,AB⊥BC,AB=3BE=3![]() ,CD=2
,CD=2![]() ,AD=2.將△ADE沿DE折起,使平面ADE⊥平面BCDE.
,AD=2.將△ADE沿DE折起,使平面ADE⊥平面BCDE.
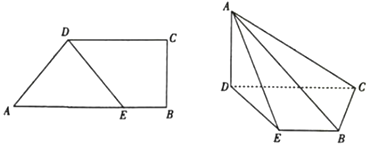
(1)證明:BC⊥平面ACD;
(2)求直線AE與平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(I)若![]() ,判斷
,判斷![]() 上的單調性;
上的單調性;
(Ⅱ)求函數![]() 上的最小值;
上的最小值;
(III)當![]() 時,是否存在正整數n,使
時,是否存在正整數n,使![]() 恒成立?若存在,求出n的最大值;若不存在,說明理由.
恒成立?若存在,求出n的最大值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某校學生參加社區服務的情況,采用按性別分層抽樣的方法進行調查.已知該校共有學生960人,其中男生560人,從全校學生中抽取了容量為![]() 的樣本,得到一周參加社區服務的時間的統計數據好下表:
的樣本,得到一周參加社區服務的時間的統計數據好下表:
超過1小時 | 不超過1小時 | |
男 | 20 | 8 |
女 | 12 | m |
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)能否有95%的把握認為該校學生一周參加社區服務時間是否超過1小時與性別有關?
(Ⅲ)以樣本中學生參加社區服務時間超過1小時的頻率作為該事件發生的概率,現從該校學生中隨機調查6名學生,試估計6名學生中一周參加社區服務時間超過1小時的人數.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】蘋果是人們日常生活中常見的營養型水果.某地水果批發市場銷售來自5個不同產地的富士蘋果,各產地的包裝規格相同,它們的批發價格(元/箱)和市場份額如下:
產地 |
|
|
|
|
|
批發價格 |
|
|
|
|
|
市場份額 |
|
|
|
|
|
市場份額亦稱“市場占有率”.指某一產品的銷售量在市場同類產品中所占比重.
(1)從該地批發市場銷售的富士蘋果中隨機抽取一箱,求該箱蘋果價格低于![]() 元的概率;
元的概率;
(2)按市場份額進行分層抽樣,隨機抽取![]() 箱富士蘋果進行檢驗,
箱富士蘋果進行檢驗,
①從產地![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;
的值;
②從這![]() 箱蘋果中隨機抽取兩箱進行等級檢驗,求兩箱產地不同的概率;
箱蘋果中隨機抽取兩箱進行等級檢驗,求兩箱產地不同的概率;
(3)由于受種植規模和蘋果品質的影響,預計明年產地![]() 的市場份額將增加
的市場份額將增加![]() ,產地
,產地![]() 的市場份額將減少
的市場份額將減少![]() ,其它產地的市場份額不變,蘋果銷售價格也不變(不考慮其它因素).設今年蘋果的平均批發價為每箱
,其它產地的市場份額不變,蘋果銷售價格也不變(不考慮其它因素).設今年蘋果的平均批發價為每箱![]() 元,明年蘋果的平均批發價為每箱
元,明年蘋果的平均批發價為每箱![]() 元,比較
元,比較![]() 的大小.(只需寫出結論)
的大小.(只需寫出結論)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com