
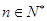 )
)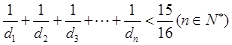 .
.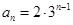 (2)見解析
(2)見解析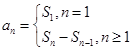 ,即可得到關于an+1,an的遞推式,證明an為等比數列,且可以知道公比,當n=1時,可以得到a1與a2之間的關系,在根據an等比數列,可以消掉a2得到首項的值,進而得到通項公式.
,即可得到關于an+1,an的遞推式,證明an為等比數列,且可以知道公比,當n=1時,可以得到a1與a2之間的關系,在根據an等比數列,可以消掉a2得到首項的值,進而得到通項公式.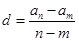 ),可以得到
),可以得到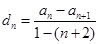 ,帶入an得到dn的通項公式.
,帶入an得到dn的通項公式.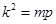 ,則m,k,p既成等差數列也是等比數列,所以三者相等,與數列{dn}中是否存在三項dm,dk,dp(不相等)矛盾,所以是不存在的.
,則m,k,p既成等差數列也是等比數列,所以三者相等,與數列{dn}中是否存在三項dm,dk,dp(不相等)矛盾,所以是不存在的.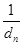 的通項公式,再利用錯位相減可以求得
的通項公式,再利用錯位相減可以求得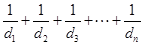 ,利用不等式的性質即可得到
,利用不等式的性質即可得到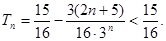 證明原式.
證明原式.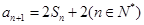 ,
,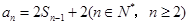 ,
,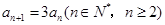 . 2分
. 2分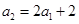 ,
,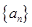 是等比數列,所以
是等比數列,所以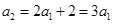 ,故
,故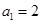 .
.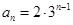 . 4分
. 4分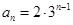 ,
,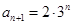
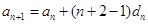 ,故:
,故: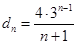 . 6分
. 6分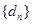 中存在三項
中存在三項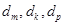 (其中
(其中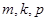 成等差數列)成等比數列,
成等差數列)成等比數列,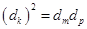 ,即:
,即: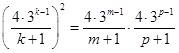 ,
,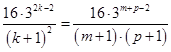 (*) 8分
(*) 8分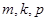 成等差數列,所以
成等差數列,所以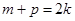 ,
,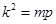 ,故
,故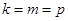 ,這與題設矛盾.
,這與題設矛盾.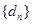 中不存在三項
中不存在三項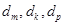 (其中
(其中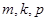 成等差數列)成等比數列.10分
成等差數列)成等比數列.10分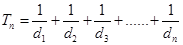 ,
,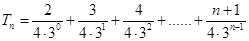 ,
,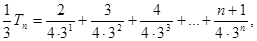 11分
11分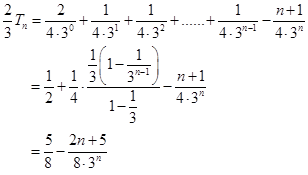 13分
13分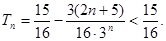 . 14分
. 14分

 一課一練課時達標系列答案
一課一練課時達標系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com