
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
分析 先求出基本事件總數n=${C}_{5}^{2}$=10,再求出取出的2支彩筆中含有紅色彩筆包含的基本事件個數m=${C}_{1}^{1}{C}_{4}^{1}$=4,由此能求出取出的2支彩筆中含有紅色彩筆的概率.
解答 解:有5支彩筆(除顏色外無差別),顏色分別為紅、黃、藍、綠、紫,
從這5支彩筆中任取2支不同顏色的彩筆,
基本事件總數n=${C}_{5}^{2}$=10,
取出的2支彩筆中含有紅色彩筆包含的基本事件個數m=${C}_{1}^{1}{C}_{4}^{1}$=4,
∴取出的2支彩筆中含有紅色彩筆的概率為p=$\frac{m}{n}$=$\frac{4}{10}=\frac{2}{5}$.
故選:C.
點評 本小題主要考查概率、古典概型、排列組合等基礎知識,考查運算求解能力和推理論證能力,是基礎題.


科目:高中數學 來源: 題型:填空題
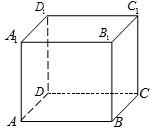 在正方體ABCD-A1B1C1D1中,給出下列結論:
在正方體ABCD-A1B1C1D1中,給出下列結論:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [1,2] | B. | [2,4] | C. | [$\sqrt{7}$-1,$\sqrt{7}$+1] | D. | [$\sqrt{5}$-1,$\sqrt{5}$+1] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,1) | B. | $[{\frac{1}{4},+∞})$ | C. | $[{\frac{3}{4},+∞})$ | D. | $({-∞,\frac{3}{4}}]$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com