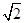【答案】
分析:法一:由
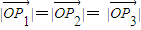
=1知O是△P
1P
2P
3的外接圓的圓心,要證△P
1P
2P
3是正三角形,只需證∠P
1OP
2=∠P
2OP
3=∠P
3OP
1即可,即需求
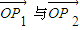
,
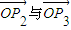
,
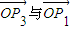
的夾角,由
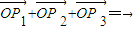
變形可出現數量積,進而求夾角
法二:用坐標法證明:以O點為坐標原點建立直角坐標系,設P
1(x
1,y
1),P
2(x
2,y
2),P
3(x
3,y
3),從而可得
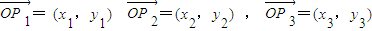
,然后由條件
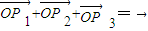
可得
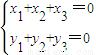
結合已知條件,用坐標表示
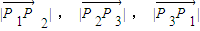 解答:
解答:證明:
法一:∵
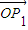
+
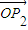
+
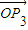
=0,∴
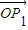
+
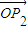
=-
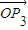
.∴|
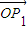
+
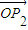
|=|-

|.
∴|
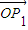
|
2+|
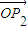
|
2+2
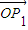
•
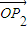
=|
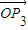
|
2.
又∵|
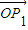
|=|
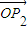
|=|
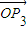
|=1,
∴
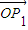
•
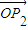
=-

.
∴|
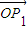
||
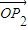
|cos∠P
1OP
2=-

,
即∠P
1OP
2=120°.
同理∠P
1OP
3=∠P
2OP
3=120°.
∴△P
1P
2P
3為等邊三角形.
法二:以O點為坐標原點建立直角坐標系,設P
1(x
1,y
1),P
2(x
2,y
2),P
3(x
3,y
3),
則
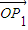
=(x
1,y
1),

=(x
2,y
2),
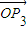
=(x
3,y
3).
由
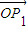
+
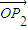
+
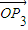
=0,
得
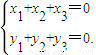
∴
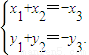
,
由|
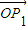
|=|
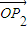
|=|
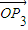
|=1,得x
12+y
12=x
22+y
22=x
32+y
32=1
∴2+2(x
1x
2+y
1y
2)=1
∴|
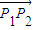
|=
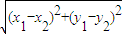
=
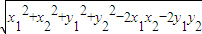
=
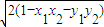
=
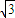
同理|
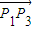
|=
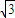
,|
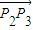
|=
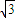
∴△P
1P
2P
3為正三角形
點評:評述:解本題的關鍵是由

+
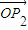
+
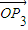
=0轉化出現向量的數量積,進而求夾角.可以用向量式表示,也可以用坐標式表示,還考查了考生的推理論證能力.

 、
、 、
、 滿足
滿足 +
+ +
+ =0,|
=0,| |=|
|=| |=|
|=| |=1.
|=1.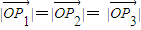 =1知O是△P1P2P3的外接圓的圓心,要證△P1P2P3是正三角形,只需證∠P1OP2=∠P2OP3=∠P3OP1即可,即需求
=1知O是△P1P2P3的外接圓的圓心,要證△P1P2P3是正三角形,只需證∠P1OP2=∠P2OP3=∠P3OP1即可,即需求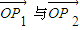 ,
,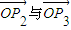 ,
,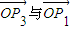 的夾角,由
的夾角,由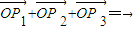 變形可出現數量積,進而求夾角
變形可出現數量積,進而求夾角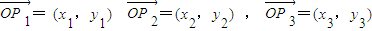 ,然后由條件
,然后由條件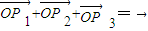 可得
可得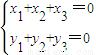 結合已知條件,用坐標表示
結合已知條件,用坐標表示
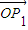 +
+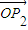 +
+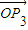 =0,∴
=0,∴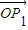 +
+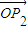 =-
=-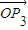 .∴|
.∴|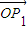 +
+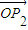 |=|-
|=|- |.
|.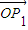 |2+|
|2+|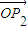 |2+2
|2+2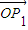 •
•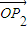 =|
=|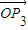 |2.
|2.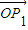 |=|
|=|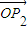 |=|
|=|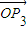 |=1,
|=1,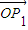 •
•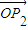 =-
=- .
.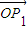 ||
||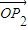 |cos∠P1OP2=-
|cos∠P1OP2=- ,
,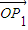 =(x1,y1),
=(x1,y1), =(x2,y2),
=(x2,y2),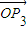 =(x3,y3).
=(x3,y3).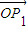 +
+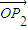 +
+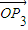 =0,
=0,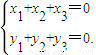 ∴
∴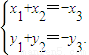 ,
,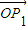 |=|
|=|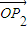 |=|
|=|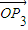 |=1,得x12+y12=x22+y22=x32+y32=1
|=1,得x12+y12=x22+y22=x32+y32=1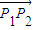 |=
|=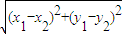
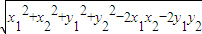
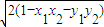 =
=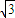
 |=
|=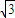 ,|
,|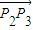 |=
|=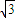
 +
+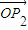 +
+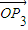 =0轉化出現向量的數量積,進而求夾角.可以用向量式表示,也可以用坐標式表示,還考查了考生的推理論證能力.
=0轉化出現向量的數量積,進而求夾角.可以用向量式表示,也可以用坐標式表示,還考查了考生的推理論證能力. 

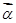 、
、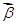 、
、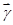 滿足
滿足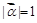 ,
, ,
,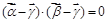 .若對每一確定的
.若對每一確定的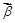 ,
,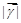 的最大值和最小值分別為
的最大值和最小值分別為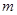 、
、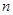 ,則對任意
,則對任意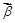 ,
,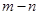 的最小值是 ( )
的最小值是 ( )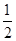 B.1 C.2 D.
B.1 C.2 D.