
分析 (1)由指數函數的單調性,判斷a>1,由最值可得a的方程,解得a=2,進而運用奇偶性的定義,計算g(-x),與g(x)比較,即可判斷g(x)的奇偶性;
(2)判斷g(x)在R上遞增,配方法求出x2-x+$\frac{3}{4}$≥$\frac{1}{2}$,計算即可得證.
解答 解:∵a>0,a≠1,a3>a2,∴a>1,
又y=ax在[1,2]上為增函數,
∴a2-a=2,解得a=2或a=-1(舍去).
∴$g(x)=1-\frac{2}{{{2^x}+1}}=\frac{{{2^x}-1}}{{{2^x}+1}}$.
(1)函數g(x)的定義域為R,
且$g({-x})=\frac{{{2^{-x}}-1}}{{{2^{-x}}+1}}=\frac{{1-{2^x}}}{{{2^x}+1}}=-\frac{{{2^x}-1}}{{{2^x}+1}}=-g(x)$,
∴函數g(x)是奇函數.
(2)證明:由復合函數的單調性得函數g(x)在R上單調遞增,
∵${x^2}-x+\frac{3}{4}={({x-\frac{1}{2}})^2}+\frac{1}{2}≥\frac{1}{2}$,
∴$g({{x^2}-x+\frac{3}{4}})≥g({\frac{1}{2}})=3-2\sqrt{2}$.
點評 本題考查函數的奇偶性和單調性的判斷及運用:證明不等式,考查指數函數的單調性及應用,運用定義是解本題的關鍵,考查運算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
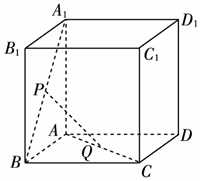 如圖所示,已知P、Q是單位正方體ABCD-A1B1C1D1的面A1B1BA和面ABCD對角線上的點,且A1P=AQ,證明:PQ∥平面BCC1B1.
如圖所示,已知P、Q是單位正方體ABCD-A1B1C1D1的面A1B1BA和面ABCD對角線上的點,且A1P=AQ,證明:PQ∥平面BCC1B1.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $a=\sqrt{3}$,b=1 | |
| B. | 函數f(x)在區間$[{\frac{π}{6},π}]$上單調遞增 | |
| C. | 函數f(x)的圖象的一個對稱中心為$({\frac{2}{3}π,0})$ | |
| D. | 不等式f(x1)f(x2)≤4取到等號時|x2-x1|的最小值為2π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com