
【題目】如圖,在平面直角坐標系xoy中,已知F1 , F2分別是橢圓E: ![]() 的左、右焦點,A,B分別是橢圓E的左、右頂點,且
的左、右焦點,A,B分別是橢圓E的左、右頂點,且 ![]() .
. 
(1)求橢圓E的離心率;
(2)已知點D(1,0)為線段OF2的中點,M 為橢圓E上的動點(異于點A、B),連接MF1并延長交橢圓E于點N,連接MD、ND并分別延長交橢圓E于點P、Q,連接PQ,設直線MN、PQ的斜率存在且分別為k1、k2 , 試問是否存在常數(shù)λ,使得k1+λk2=0恒成立?若存在,求出λ的值;若不存在,說明理由.
【答案】
(1)解:∵ ![]() ,∴
,∴ ![]() .
.
∴a+c=5(a﹣c),化簡得2a=3c,
故橢圓E的離心率為 ![]()
(2)解:存在滿足條件的常數(shù)λ, ![]() .
.
∵點D(1,0)為線段OF2的中點,∴c=2,從而a=3, ![]() ,
,
左焦點F1(﹣2,0),橢圓E的方程為 ![]() .
.
設M(x1,y1),N(x2,y2),P(x3,y3),Q(x4,y4),則直線MD的方程為 ![]() ,
,
代入橢圓方程 ![]() ,整理得,
,整理得, ![]() .
.
∵ ![]() ,∴
,∴ ![]() .
.
從而 ![]() ,故點
,故點 ![]() .同理,點
.同理,點 ![]() .
.
∵三點M、F1、N共線,∴ ![]() ,從而x1y2﹣x2y1=2(y1﹣y2).
,從而x1y2﹣x2y1=2(y1﹣y2).
從而 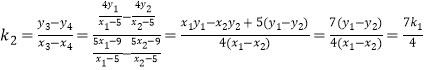 .
.
故 ![]() ,從而存在滿足條件的常數(shù)λ,
,從而存在滿足條件的常數(shù)λ, ![]()
【解析】(1)由 ![]() ,得
,得 ![]() ,從而有a+c=5(a﹣c),結合離心率定義即可求得答案;(2)由點D(1,0)為線段OF2的中點可求得c值,進而可求出a值、b值,得到橢圓方程,設M(x1 , y1),N(x2 , y2),P(x3 , y3),Q(x4 , y4),則直線MD的方程為
,從而有a+c=5(a﹣c),結合離心率定義即可求得答案;(2)由點D(1,0)為線段OF2的中點可求得c值,進而可求出a值、b值,得到橢圓方程,設M(x1 , y1),N(x2 , y2),P(x3 , y3),Q(x4 , y4),則直線MD的方程為 ![]() ,與橢圓方程聯(lián)立及韋達定理可把P、Q坐標用M、N坐標表示出來,再根據(jù)三點M、F1、N共線及斜率公式可得k1、k2間的關系式,由此可得答案.
,與橢圓方程聯(lián)立及韋達定理可把P、Q坐標用M、N坐標表示出來,再根據(jù)三點M、F1、N共線及斜率公式可得k1、k2間的關系式,由此可得答案.


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:高中數(shù)學 來源: 題型:
【題目】設集合A={x∈R|2x﹣8=0},B={x∈R|x2﹣2(m+1)x+m2=0}
(1)若m=4,求A∪B;
(2)若A∪B=A,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】祖暅是南北朝時代的偉大科學家,5世紀末提出體積計算原理,即祖暅原理:“冪勢既同,則積不容異”.意思是:夾在兩個平行平面之間的兩個幾何體,被平行于這兩個平面的任何一個平面所截,如果截面面積都相等,那么這兩個幾何體的體積一定相等.現(xiàn)有以下四個幾何體:圖①是從圓柱中挖出一個圓錐所得的幾何體;圖②、圖③、圖④分別是圓錐、圓臺和半球,則滿足祖暅原理的兩個幾何體為( )
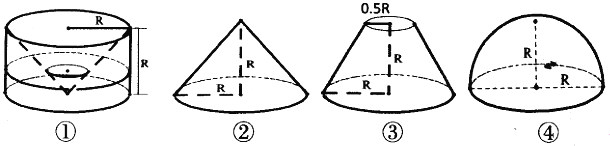
A. ①② B. ①③ C. ②④ D. ①④
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=3x2﹣2ax﹣b,其中a,b是實數(shù).
(1)若不等式f(x)≤0的解集是[0,6],求ab的值;
(2)若b=3a,對任意x∈R,都有f(x)≥0,且存在實數(shù)x,使得f(x)≤2﹣ ![]() a,求實數(shù)a的取值范圍;
a,求實數(shù)a的取值范圍;
(3)若方程有一個根是1,且a,b>0,求 ![]() 的最小值,及此時a,b的值.
的最小值,及此時a,b的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線y2=4x的焦點為F,過點F的直線交拋物線于A,B兩點.
(1)若 ![]() =3
=3 ![]() ,求直線AB的斜率;
,求直線AB的斜率;
(2)設點M在線段AB上運動,原點O關于點M的對稱點為C,求四邊形OACB面積的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某地區(qū)山體大面積滑坡,政府準備調運一批賑災物資共裝26輛車,從某市出發(fā)以v(km/h)的速度勻速直達災區(qū),如果兩地公路長400km,且為了防止山體再次坍塌,每兩輛車的間距保持在( ![]() )2km.(車長忽略不計)設物資全部運抵災區(qū)的時間為y小時,請建立y關于每車平均時速v(km/h)的函數(shù)關系式,并求出車輛速度為多少千米/小時,物資能最快送到災區(qū)?
)2km.(車長忽略不計)設物資全部運抵災區(qū)的時間為y小時,請建立y關于每車平均時速v(km/h)的函數(shù)關系式,并求出車輛速度為多少千米/小時,物資能最快送到災區(qū)?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】山西某公司有一批專業(yè)技術人員,對他們進行年齡狀況和接受教育程度(本科學歷)的調查,其結果(人數(shù)分布)如表:
學歷 | 35歲以下 | 35 | 50歲以上 |
本科 | 80 | 30 | 20 |
研究生 |
| 20 |
|
(Ⅰ)用分層抽樣的方法在![]() 歲年齡段的專業(yè)技術人員中抽取一個容量為10的樣本,將該樣本看成一個總體,從中任取3人,求至少有1人的學歷為研究生的概率;
歲年齡段的專業(yè)技術人員中抽取一個容量為10的樣本,將該樣本看成一個總體,從中任取3人,求至少有1人的學歷為研究生的概率;
(Ⅱ)在這個公司的專業(yè)技術人員中按年齡狀況用分層抽樣的方法抽取![]() 個人,其中35歲以下48人,50歲以上10人,再從這
個人,其中35歲以下48人,50歲以上10人,再從這![]() 個人中隨機抽取出1人,此人的年齡為50歲以上的概率為
個人中隨機抽取出1人,此人的年齡為50歲以上的概率為![]() ,求
,求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知{an}是一個等差數(shù)列,且a2=1,a5=﹣5.
(Ⅰ)求{an}的通項an;
(Ⅱ)求{an}前n項和Sn的最大值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com