
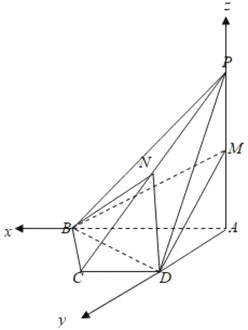
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是一個直角梯形,其中
是一個直角梯形,其中![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,點M和點N分別為
,點M和點N分別為![]() 和
和![]() 的中點.
的中點.
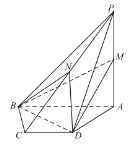
(1)證明:直線![]() 平面
平面![]() ;
;
(2)求直線![]() 和平面
和平面![]() 所成角的余弦值;
所成角的余弦值;
(3)求二面角![]() 的正弦值;
的正弦值;
(4)求點P到平面![]() 的距離;
的距離;
(5)設點N在平面![]() 內的射影為點H,求線段
內的射影為點H,求線段![]() 的長.
的長.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ;(5)
;(5)![]()
【解析】
(1)以![]() 為原點,建立空間直角坐標系,利用向量法,證明
為原點,建立空間直角坐標系,利用向量法,證明![]() 與平面
與平面![]() 的法向量垂直,從而證明直線
的法向量垂直,從而證明直線![]() 平面
平面![]() .
.
(2)求出平面![]() 的法向量,利用向量法,求出直線
的法向量,利用向量法,求出直線![]() 和平面
和平面![]() 所成角的余弦值.
所成角的余弦值.
(3)求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,利用向量法,求出二面角
的法向量,利用向量法,求出二面角![]() 的正弦值.
的正弦值.
(4)求出![]() 的坐標,再求出平面
的坐標,再求出平面![]() 的法向量
的法向量![]() ,利用向量法,求出點
,利用向量法,求出點![]() 到平面
到平面![]() 的距離;
的距離;
(5)設點![]() 在平面
在平面![]() 內的射影為點
內的射影為點![]() ,從而表示出
,從而表示出![]() 的坐標,求出
的坐標,求出![]() 到平面
到平面![]() 的距離
的距離![]() ,列出方程組,求出
,列出方程組,求出![]() 點坐標,從而求出
點坐標,從而求出![]() 的長度.
的長度.
(1)四棱錐![]() ,底面
,底面![]() 是一個直角梯形,
是一個直角梯形,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 為原點,
為原點,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,建立空間直角坐標系,
軸,建立空間直角坐標系,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量
的法向量![]() ,
,
所以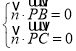 ,
,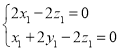 ,
,
取![]() ,則
,則![]() ,
,
所以![]() ,
,![]() 平面
平面![]() ,
,
所以直線![]() 平面
平面![]() .
.
(2)![]() ,
,![]() ,
,![]() ,
,![]()
設平面![]() 的法向量
的法向量![]() ,
,
則 ,即
,即 ,
,
取![]() ,則
,則![]() ,
,
設直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
則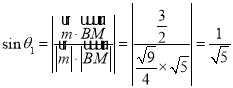 ,
,
所以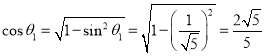 ,
,
所以直線![]() 與平面
與平面![]() 所成角的余弦值為
所成角的余弦值為![]() .
.
(3)設平面![]() 的法向量為
的法向量為![]() ,
,
則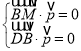 ,即
,即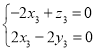 ,
,
取![]() ,得
,得![]() ,
,
平面![]() 的法向量
的法向量![]() ,
,
設二面角![]() 的平面角為
的平面角為![]() ,
,
則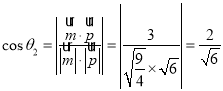 ,
,
所以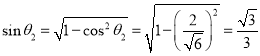 ,
,
所以二面角![]() 的正弦值為
的正弦值為![]() .
.
(4)![]() ,平面
,平面![]() 的法向量
的法向量![]() ,
,
所以點![]() 到平面
到平面![]() 的距離為
的距離為
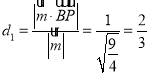 .
.
(5)設點![]() 在平面
在平面![]() 的射影為點
的射影為點![]() ,
,
則![]() ,
,
所以點![]() 到平面
到平面![]() 的距離為
的距離為 ,
,
根據 ,得
,得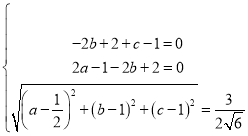
解得![]() ,
,![]() ,
,![]() ,或者
,或者![]() ,
,![]() ,
,![]() (舍)
(舍)
所以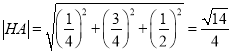 .
.


 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:高中數學 來源: 題型:
【題目】如圖,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,直角梯形
,直角梯形![]() 通過直角梯形
通過直角梯形![]() 以直線
以直線![]() 為軸旋轉得到,且使得平面
為軸旋轉得到,且使得平面![]() 平面
平面![]() .
. ![]() 為線段
為線段![]() 的中點,
的中點, ![]() 為線段
為線段![]() 上的動點.
上的動點.

(![]() )求證:
)求證: ![]() .
.
(![]() )當點
)當點![]() 滿足
滿足![]() 時,求證:直線
時,求證:直線![]() 平面
平面![]() .
.
(![]() )當點
)當點![]() 是線段
是線段![]() 中點時,求直線
中點時,求直線![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2+x-6y+m=0與直線l:x+2y-3=0.
(1)若直線l與圓C沒有公共點,求m的取值范圍;
(2)若直線l與圓C相交于P、Q兩點,O為原點,且OP⊥OQ,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:①![]() 越小,X與Y有關聯的可信度越小;②若兩個隨機變量的線性相關性越強,則相關系數r的值越接近于1;③“若
越小,X與Y有關聯的可信度越小;②若兩個隨機變量的線性相關性越強,則相關系數r的值越接近于1;③“若![]() ,則
,則![]() 類比推出,“若
類比推出,“若![]() ,則
,則![]() ;④命題“有些有理數是無限循環小數,整數是有理數,所以整數是無限循環小數”是假命題,推理錯誤的原因是使用了“三段論”,推理形式錯誤.其中說法正確的有( )個
;④命題“有些有理數是無限循環小數,整數是有理數,所以整數是無限循環小數”是假命題,推理錯誤的原因是使用了“三段論”,推理形式錯誤.其中說法正確的有( )個
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某新上市的電子產品舉行為期一個星期(7天)的促銷活動,規定購買該電子產品可免費贈送禮品一份,隨著促銷活動的有效開展,第五天工作人員對前五天中參加活動的人數進行統計,![]() 表示第
表示第![]() 天參加該活動的人數,得到統計表格如下:
天參加該活動的人數,得到統計表格如下:
| 1 | 2 | 3 | 4 | 5 |
| 4 | 6 | 10 | 23 | 22 |
(1)若![]() 與
與![]() 具有線性相關關系,請根據上表提供的數據,用最小二乘法求出
具有線性相關關系,請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)預測該星期最后一天參加該活動的人數(按四舍五入取到整數).
參考公式: ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com