
分析 根據圓的方程,找出圓心坐標和半徑r,根據平移規律“上加下減,左加右減”表示出平移后直線的方程,根據平移后直線與圓相切,可得圓心到直線的距離等于圓的半徑,利用點到直線的距離公式列出關于m的方程,求出方程的解即可得到m的值.
解答 解:圓x2+y2=1的圓心坐標為(0,0),半徑r=1,
直線3x+4y+m=0向左平移2個單位,再向上平移3個單位后解析式為:
3(x-2)+4(y-3)+m=0,即3x+4y+m-18=0,
由此時直線與圓相切,可得圓心到直線的距離d=$\frac{|m-18|}{5}$=1,
解得:m=23或13.
故答案為23或13.
點評 此題考查了直線與圓的位置關系,涉及的知識有:圓的標準方程,點到直線的距離公式,以及平移規律,當直線與圓相切時,圓心到直線的距離等于圓的半徑,熟練掌握此性質及平移規律是解本題的關鍵.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|x<-1或x>2} | B. | {x|x<-2或x>1} | C. | {x|-2<x<1} | D. | {x|-1<x<2} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
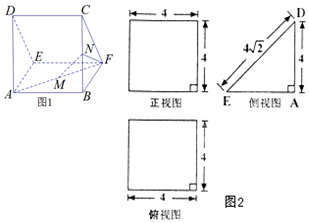 一個多面體的直觀圖(圖1)及三視圖(圖2)如圖所示,其中M、N分別是AF、BC的中點,
一個多面體的直觀圖(圖1)及三視圖(圖2)如圖所示,其中M、N分別是AF、BC的中點,查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
| 對服務好評 | 對服務不滿意 | 合計 | |
| 對商品好評 | a=80 | b=40 | 120 |
| 對商品不滿意 | c=70 | d=10 | 80 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com