
【題目】自新型冠狀病毒疫情爆發以來,人們時刻關注疫情,特別是治愈率,治愈率![]() 累計治愈人數/累計確診人數,治愈率的高低是“戰役”的重要數據,由于確診和治愈人數在不斷變化,那么人們就非常關心第
累計治愈人數/累計確診人數,治愈率的高低是“戰役”的重要數據,由于確診和治愈人數在不斷變化,那么人們就非常關心第![]() 天的治愈率,以此與之前的治愈率比較,來推斷在這次“戰役”中是否有了更加有效的手段,下面是一段計算治愈率的程序框圖,請同學們選出正確的選項,分別填入①②兩處,完成程序框圖.( )
天的治愈率,以此與之前的治愈率比較,來推斷在這次“戰役”中是否有了更加有效的手段,下面是一段計算治愈率的程序框圖,請同學們選出正確的選項,分別填入①②兩處,完成程序框圖.( )
![]() :第
:第![]() 天新增確診人數;
天新增確診人數;![]() :第
:第![]() 天新增治愈人數;
天新增治愈人數;![]() :第
:第![]() 天治愈率
天治愈率
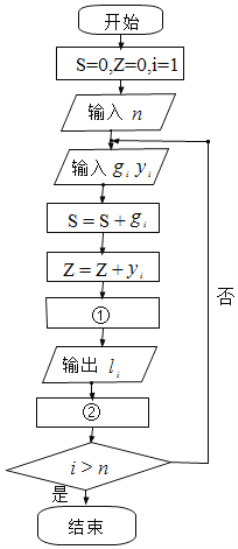
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中,![]() 是邊長為2的等邊三角形,
是邊長為2的等邊三角形,![]() ,
,![]() ,
,![]() .
.
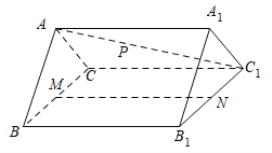
(1)證明:平面![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點,
的中點,![]() 是線段
是線段![]() 上的動點,若二面角
上的動點,若二面角![]() 的平面角的大小為
的平面角的大小為![]() ,試確定點
,試確定點![]() 的位置.
的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】科赫曲線是一種外形像雪花的幾何曲線,一段科赫曲線可以通過下列操作步驟構造得到,任畫一條線段,然后把它均分成三等分,以中間一段為邊向外作正三角形,并把中間一段去掉,這樣,原來的一條線段就變成了4條小線段構成的折線,稱為“一次構造”;用同樣的方法把每條小線段重復上述步驟,得到16條更小的線段構成的折線,稱為“二次構造”,…,如此進行“![]() 次構造”,就可以得到一條科赫曲線.若要在構造過程中使得到的折線的長度達到初始線段的1000倍,則至少需要通過構造的次數是( ).(取
次構造”,就可以得到一條科赫曲線.若要在構造過程中使得到的折線的長度達到初始線段的1000倍,則至少需要通過構造的次數是( ).(取![]() ,
,![]() )
)

A.16B.17C.24D.25
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,側面
中,側面![]() 是邊長為2的等邊三角形且垂直于底面
是邊長為2的等邊三角形且垂直于底面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點.
的中點.
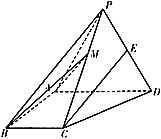
(1)求證:直線![]() 平面
平面![]() ;
;
(2)點![]() 在棱
在棱![]() 上,且二面角
上,且二面角![]() 的余弦值為
的余弦值為![]() ,求直線
,求直線![]() 與底面
與底面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,已知圓
中,已知圓![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數).以
為參數).以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,直線
軸的非負半軸為極軸建立極坐標系,直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() :
:![]() 與圓
與圓![]() 的交點為
的交點為![]() 、
、![]() 兩點,
兩點,![]() 與直線
與直線![]() 的交點為
的交點為![]() .
.
(1)求圓![]() 的極坐標方程;
的極坐標方程;
(2)求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是民航部門統計的某年春節期間:中國民航出入境航線方面TOP10出入境國家和地區的旅客量以及相比上年同期變化幅度的數據統計圖表,根據圖表,下面敘述不正確的是( )
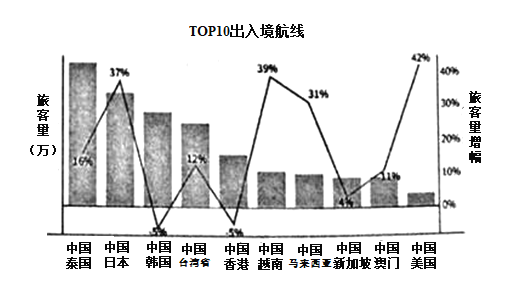
A.東南亞仍是人們出境旅游的首選
B.臺灣和澳門均有超過一成的同比增長
C.越南和美國排在人們出境旅游選擇的前兩位
D.中-韓航線雖依然位列出入境國家和地區第三甲,但旅客量卻較去年出現負增長
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com