【題目】為維護交通秩序，防范電動自行車被盜，天津市公安局決定，開展二輪電動自行車免費登記、上牌照工作.電動自行車牌照分免費和收費(安裝防盜裝置)兩大類，群眾可以 自愿選擇安裝.已知甲、乙、丙三個不同類型小區的人數分別為15000，15000，20000.交管部門為了解社區居民意愿，現采用分層抽樣的方法從中抽取10人進行電話訪談.
（Ⅰ）應從甲小區和丙小區的居民中分別抽取多少人?
（Ⅱ）設從甲小區抽取的居民為
，丙小區抽取的居民為
.現從甲小區和丙小區已抽取的居民中隨機抽取2人接受問卷調查.
（ⅰ）試用所給字母列舉出所有可能的抽取結果；
（ⅱ）設
為事件“抽取的2人來自不同的小區”，求事件發生的概率.
【答案】（Ⅰ）甲小區抽取3人、丙小區抽取4人．（Ⅱ）(i)見解析(ii)
．
【解析】
（Ⅰ）利用分層抽樣的性質能求出應從甲、乙、丙三個不同類型小區中分別抽取得3人，3人，4人．
（Ⅱ）（ⅰ）從甲小區抽取的3位居民為
，丙小區抽取的4人分別為
利用列舉法能求出所有可能結果．
（ⅱ）由（ⅰ）可得基本事件總個數，
為事件“抽取的2人來自不同的小區”利用列舉法能求出事件發生的概率．
（Ⅰ）因為三個小區共有50000名居民，所以運用分層抽樣抽取甲、丙小區的人數分別為：甲小區：
（人）；
丙小區：
（人）.
即甲小區抽取3人、丙小區抽取4人．
（Ⅱ）(i)設甲小區抽取的3人分別為，丙小區抽取的4人分別為，
則從7名居民中抽2名居民共有21種可能情況：
,
(ii)顯然，事件包含的基本事件有:
共12種，
所以
.
故抽取的2人來自不同的小區的概率為．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝sin（2x+
）+cos（2x﹣
）+cos2x﹣sin2x，x∈R．
（1）求函數f（x）的最小正周期及單調遞增區間；
（2）求函數f（x）在區間[﹣
]上的最大值和最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有甲乙兩個班級進行數學考試，按照大于等于85分為優秀，85分以下為非優秀統計成績后，得到如下的列聯表.
| 優秀 | 非優秀 | 總計 |
甲班 | 10 | ||
乙班 | 30 | ||
總計 | 105 |
已知在全部105人中隨機抽取1人為優秀的概率為
.
(1)請完成上面的列聯表；（把列聯表自己畫到答題卡上）
(2)根據列聯表的數據，若按95%的可靠性要求，能否認為“成績與班級有關系”？
參考公式：
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，
、
分別為橢圓
的焦點，橢圓的右準線
與
軸交于
點，若
，且
.
（Ⅰ）求橢圓的方程；
（Ⅱ）過、作互相垂直的兩直線分別與橢圓交于
、
、
、
四點，求四邊形
面積的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某醫藥研究所開發的一種新藥，如果成年人按規定的劑量服用，據監測：服藥后每毫升血液中的含藥量y(微克)與時間t(小時)之間近似滿足如圖所示的曲線．
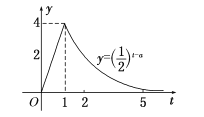
(1)寫出第一次服藥后，y與t之間的函數關系式y＝f(t)；
(2)據進一步測定：每毫升血液中含藥量不少于0.25微克時，治療有效．求服藥一次后治療有效的時間是多長？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知以點P為圓心的圓經過點A（－1，0）和B（3，4），線段AB的垂直平分線交圓P于點C和D，且|CD|＝
.
（1）求直線CD的方程；
（2）求圓P的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
的前
項和為
，滿足
，
，數列
滿足
，，且
.
（1）求數列的通項公式；
（2）求證：數列
是等差數列，求數列的通項公式；
（3）若
，數列
的前項和為
，對任意的，都有
，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給定一個由
個小正方形拼成的棋盤形方格，這些小正方形的顏色黑白相間（如圖）.
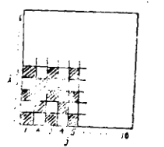
現定義一種運算A：把位于第i行的所有小正方形和位于第j列的所有小正方形都換成相反的顏色，即黑色的小正方形換成白色的，白色的小正方形換成黑色的，這里
．我們把A稱為在位于第i行第j列上的小正方形上的一次運算.試問：能否經過若干次上述運算把棋盤上的所有小正方形全部換成同一種顏色？證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
