
分析 (1)當n≥2時,利用an=An-An-1可得an=2n-1,再驗證n=1的情況,即可求得數列{an}的通項公式;
(2)由題意知:${c_n}=\frac{a_n}{2^n}=\frac{2n-1}{2^n}$,利用錯位相減法即可求得數列{cn}的前n項和Cn;
(3)利用基本不等式可得${b_n}=\frac{2n-1}{2n+1}+\frac{2n+1}{2n-1}$>$2\sqrt{\frac{2n-1}{2n+1}•\frac{2n+1}{2n-1}}=2$,可得Bn=b1+b2+…+bn>2n;再由bn=$\frac{2n-1}{2n+1}+\frac{2n+1}{2n-1}=1-\frac{2}{2n+1}+1+\frac{2}{2n-1}=2+\frac{2}{2n-1}-\frac{2}{2n+1}$,累加可${B_n}=(2+\frac{2}{1}-\frac{2}{3})+(2+\frac{2}{3}-\frac{2}{5})+…+(2+\frac{2}{2n-1}-\frac{2}{2n+1})=2n+2-\frac{2}{2n+1}<2n+2$,
于是可證明:$2n<{B_n}<2n+2({n∈{N^*}})$.
解答 (本小題滿分13分)
解:( I)當n≥2時,${A_n}={n^2}$,${A_{n-1}}={(n-1)^2}$,
兩式相減:an=An-An-1=2n-1;
當n=1時,a1=A1=1,也適合an=2n-1,
故數列{an}的通項公式為an=2n-1;.…(3分)
( II)由題意知:${c_n}=\frac{a_n}{2^n}=\frac{2n-1}{2^n}$,Cn=c1+c2+…+cn,
${C_n}=\frac{1}{2^1}+\frac{3}{2^2}+\frac{5}{2^3}+…+\frac{2n-1}{2^n}$,$\frac{C_n}{2}=\frac{1}{2^2}+\frac{3}{2^3}+\frac{5}{2^4}+…+\frac{2n-1}{{{2^{n+1}}}}$,
兩式相減可得:$\frac{C_n}{2}=\frac{1}{2^1}+\frac{2}{2^2}+\frac{2}{2^3}+…+\frac{2}{2^n}-\frac{2n-1}{{{2^{n+1}}}}$,…(4分)
即$\frac{C_n}{2}=\frac{1}{2}+(\frac{1}{2^1}+\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{{{2^{n-1}}}})-\frac{2n-1}{{{2^{n+1}}}}$,$\frac{C_n}{2}=\frac{1}{2}+(1-\frac{1}{{{2^{n-1}}}})-\frac{2n-1}{{{2^{n+1}}}}$,${C_n}=3-\frac{2n+3}{2^n}$.…(7分)
( III)${b_n}=\frac{2n-1}{2n+1}+\frac{2n+1}{2n-1}$,顯然$\frac{2n-1}{2n+1}+\frac{2n+1}{2n-1}>2\sqrt{\frac{2n-1}{2n+1}•\frac{2n+1}{2n-1}}=2$,
即bn>2,Bn=b1+b2+…+bn>2n; …(9分)
另一方面,$\frac{2n-1}{2n+1}+\frac{2n+1}{2n-1}=1-\frac{2}{2n+1}+1+\frac{2}{2n-1}=2+\frac{2}{2n-1}-\frac{2}{2n+1}$,
即${b_1}=2+\frac{2}{1}-\frac{2}{3}$,${b_2}=2+\frac{2}{3}-\frac{2}{5}$,…,${b_n}=2+2({\frac{1}{2n-1}-\frac{1}{2n+1}})$,${B_n}=(2+\frac{2}{1}-\frac{2}{3})+(2+\frac{2}{3}-\frac{2}{5})+…+(2+\frac{2}{2n-1}-\frac{2}{2n+1})=2n+2-\frac{2}{2n+1}<2n+2$,
即:2n<Bn<2n+2.…(13分)
點評 本題考查數列遞推式的應用,突出考查錯位相減法求和與累加法求和的綜合運用,考查推理與運算能力,屬于難題.


科目:高中數學 來源: 題型:選擇題
| A. | f(x)是奇函數,則在(0,+∞)上是增函數 | |
| B. | f(x)是偶函數,則在(0,+∞)上是減函數 | |
| C. | f(x)既不是奇函數也不是偶函數,且在(0,+∞)上是增函數 | |
| D. | f(x)既不是奇函數也不是偶函數,且在(0,+∞)上是減函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
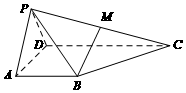 在四棱錐P-ABCD中,平面PAD⊥平面ABCD,△PAD為等邊三角形,$AB=AD=\frac{1}{2}CD$,AB⊥AD,AB∥CD,點M是PC的中點.
在四棱錐P-ABCD中,平面PAD⊥平面ABCD,△PAD為等邊三角形,$AB=AD=\frac{1}{2}CD$,AB⊥AD,AB∥CD,點M是PC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{4}{3}$ | B. | $-\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com