
【題目】若函數![]() 對任意
對任意![]() ,都有
,都有![]() ,則稱函數
,則稱函數![]() 是“以
是“以![]() 為界的類斜率函數”.
為界的類斜率函數”.
(1)試判斷函數![]() 是否為“以
是否為“以![]() 為界的類斜率函數”;
為界的類斜率函數”;
(2)若實數![]() ,且函數
,且函數![]() 是“以
是“以![]() 為界的類斜率函數”,求
為界的類斜率函數”,求![]() 的取值范圍.
的取值范圍.
 優生樂園系列答案
優生樂園系列答案 新編小學單元自測題系列答案
新編小學單元自測題系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() x3﹣x2+x.
x3﹣x2+x.
(1)求函數f(x)在[﹣1,2]上的最大值和最小值;
(2)若函數g(x)=f(x)﹣4x,x∈[﹣3,2],求g(x)的單調區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知R上的奇函數f(x)和偶函數g(x)滿足f(x)+g(x)=ax﹣a﹣x+2(a>0,且a≠1),若g(2)=a,則f(2)的值為(
A.![]()
B.2
C.![]()
D.a2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代的數學名著,書中有如下問題:“今有五人分五錢,令上二人所得與下三人等.問各得幾何.”其意思為“已知甲、乙、丙、丁、戊五人分5錢,甲、乙兩人所得與丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差數列.問五人各得多少錢?”(“錢”是古代的一種重量單位).這個問題中,甲所得為( )
A.![]() 錢
錢
B.![]() 錢
錢
C.![]() 錢
錢
D.![]() 錢
錢
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用長為90cm,寬為48cm的長方形鐵皮做一個無蓋的容器,先在四角分別截去一個小正方形,然后把四邊翻轉90°角,再焊接而成(如圖),問該容器的高為多少時,容器的容積最大?最大容積是多少? 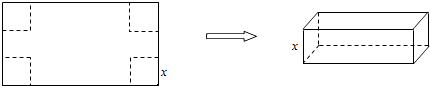
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,底面
中,底面![]() 是矩形,
是矩形, ![]() 平面
平面![]() ,
, ![]() 是等腰三角形,
是等腰三角形, ![]() ,
, ![]() 是
是![]() 的一個三等分點(靠近點
的一個三等分點(靠近點![]() ),
),![]() 的延長線與
的延長線與![]() 的延長線交于點
的延長線交于點![]() ,連接
,連接![]() .
.
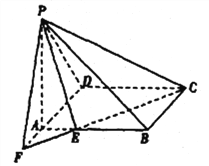
(1)求證: ![]() ;
;
(2)求證:在線段![]() 上可以分別找到兩點
上可以分別找到兩點![]() ,
, ![]() ,使得直線
,使得直線![]() 平面
平面![]() ,并分別求出此時
,并分別求出此時![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com