
(本小題滿分13分)已知函數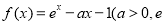 為自然對數的底數)
為自然對數的底數)
(1)求函數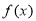 的最小值;
的最小值;
(2)若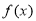 ≥0對任意的x∈R恒成立,求實數a的值;
≥0對任意的x∈R恒成立,求實數a的值;
(3)在(2)的條件下,證明:
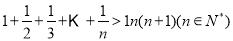
(1)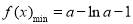 (2)
(2)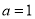 (3)
(3)
【解析】
試題分析:(1)求導,討論函數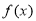 的單調性,可求函數
的單調性,可求函數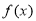 的最小值;
的最小值;
(2)問題即為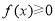 對任意的
對任意的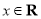 恒成立,即在
恒成立,即在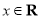 上,
上,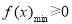 .,設
.,設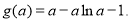 ,即解
,即解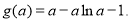 討論函數
討論函數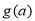 的單調性,可得
的單調性,可得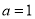
(3)(2)得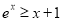 ,即
,即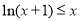 ,當且僅當
,當且僅當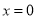 時,等號成立,令
時,等號成立,令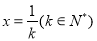
則,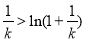 即
即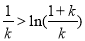 ,所以
,所以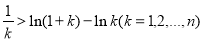 ,累加即可得證
,累加即可得證
試題解析:(1)由題意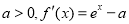 ,
,
由 得
得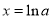 .
.
當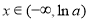 時,
時, 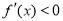 ;當
;當 時,
時,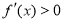 .
.
∴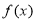 在
在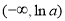 單調遞減,在
單調遞減,在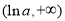 單調遞增
單調遞增
即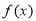 在
在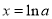 處取得極小值,且為最小值,
處取得極小值,且為最小值,
其最小值為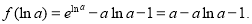
(2)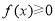 對任意的
對任意的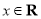 恒成立,即在
恒成立,即在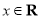 上,
上,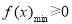 .
.
由(1),設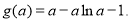 ,所以
,所以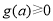 .
.
由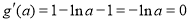 得
得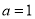 .
.
易知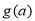 在區間
在區間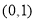 上單調遞增,在區間
上單調遞增,在區間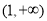 上單調遞減,
上單調遞減,
∴ 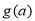 在
在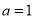 處取得最大值,而
處取得最大值,而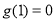 .
.
因此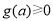 的解為
的解為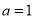 ,∴
,∴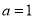
(3)由(2)得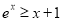 ,即
,即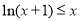 ,當且僅當
,當且僅當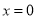 時,等號成立,令
時,等號成立,令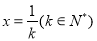
則,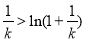 即
即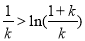 ,所以
,所以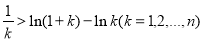
累加得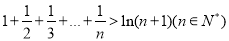
考點:利用導數研究函數的性質,利用導數證明有關命題


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:高中數學 來源:2014-2015學年湖南省瀏陽、醴陵、攸縣三校高三聯考理科數學試卷(解析版) 題型:選擇題
設Sn為等差數列{an}的前n項和,若a1=1,a3=5,Sk+2﹣Sk=36,則k的值為( )
A.8 B.7 C.6 D.5
查看答案和解析>>
科目:高中數學 來源:2014-2015學年河北省保定市高三上學期12月份聯考理科數學試卷(解析版) 題型:選擇題
若將函數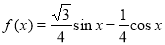 的圖象向右平移
的圖象向右平移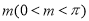 個單位長度,得到的圖象關于原點對稱,則
個單位長度,得到的圖象關于原點對稱,則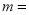 ( )
( )
A.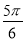 B.
B.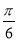 C.
C.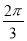 D.
D.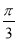
查看答案和解析>>
科目:高中數學 來源:2014-2015學年安徽省江淮名校高三第二次聯考文科數學試卷(解析版) 題型:選擇題
已知等差數列{an}的前n項之和是Sn,則-am<a1<-am+l是Sm>0,Sm+1<0的( )
A.充分必要條件
B.必要不充分條件
C.充分不必要條件
D.既不充分也不毖要
查看答案和解析>>
科目:高中數學 來源:2014-2015學年安徽省江淮名校高三第二次聯考理科數學試卷(解析版) 題型:填空題
已知集合M= ,對于任意實數對
,對于任意實數對 ,存在實數對(x1,y2)
,存在實數對(x1,y2)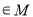 使得x1x2+y1y2=0成立,則稱集命M是:“孿生對點集”-給出下列五個集合-;
使得x1x2+y1y2=0成立,則稱集命M是:“孿生對點集”-給出下列五個集合-;
①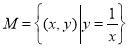
②
③
④
⑤
其中不是“孿生對點集”的序號是 。
查看答案和解析>>
科目:高中數學 來源:2014-2015學年安徽省江淮名校高三第二次聯考理科數學試卷(解析版) 題型:選擇題
已知函數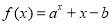 ,的零點
,的零點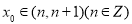 ,其中常數a,b滿足2a =3,3b =2,則n的值是( )
,其中常數a,b滿足2a =3,3b =2,則n的值是( )
A.-2 B.-l C.0 D.1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com