Question

【題目】在直角坐標系中，橢圓 的左、右焦點分別為，點在橢圓上且軸，直線交軸于點， ， 為橢圓的上頂點， 的面積為1.

（1）求橢圓的方程；

（2）過的直線交橢圓于， ，且滿足，求的面積.

Answer 1

【答案】（1）；（2）

【解析】【試題分析】(1)將代入橢圓方程,求得點的縱坐標,利用中點的坐標建立一個方程.利用的面積聯立第二個方程,結合,解方程組求得的值,即求得橢圓的方程.(2)對兩邊平方化簡得.當直線斜率不存在時,求得兩點的坐標,驗證可知不符合題意.當直線斜率存在時,設出直線方程,聯立直線方程和橢圓的方程,消去后斜率韋達定理,利用得,列方程求得直線的斜率.最后利用弦長公式和點到直線距離公式求得三角形面積.

【試題解析】

（1）設，由題意可得，即.

∵是的中位線，且，∴，即，整理得.①

又由題知， 為橢圓的上頂點，∴的面積，

整理得，即，②

聯立①②可得，變形得，解得，進而.

∴橢圓的方程為.

(2)由可得，兩邊平方整理得.

直線斜率不存在時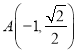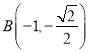， ， ，不滿足.

直線斜率存在時，設直線的方程為， ， ，

聯立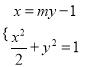，消去，得，

∴， ，（*）

由得.

將， 代入整理得，

展開得，

將（*）式代入整理得，解得，

∴， ，

的面積為 ，

代入計算得，即的面積為.