
 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
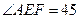 °
°
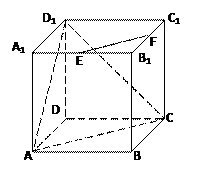
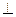 平面BCE;
平面BCE; 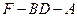 的大小。
的大小。查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
查看答案和解析>>
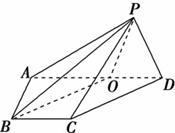
科目:高中數(shù)學 來源:不詳 題型:解答題
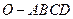 中,底面
中,底面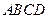 為菱形,
為菱形,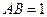 ,
,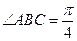 ,
,  ,
, 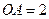 ,
,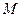 為
為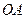 的中點,
的中點,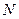 為
為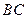 的中點
的中點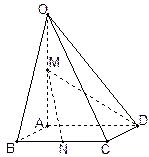
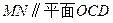
 ;
;查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
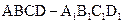 中,E是棱
中,E是棱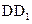 的中點.
的中點.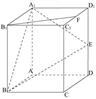
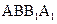 所成的角的正弦值;
所成的角的正弦值;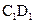 上是否存在一點F,使
上是否存在一點F,使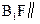 平面
平面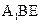 ?證明你的結論.
?證明你的結論. 查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
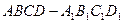 中,底面
中,底面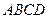 是
是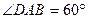
 的菱形,
的菱形,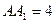 ,
,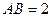 ,點
,點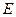 在棱
在棱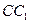 上,點
上,點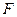 是棱
是棱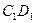 的中點.
的中點.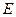 是
是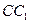 的中點,求證:
的中點,求證: ;
;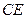 的長度,使得
的長度,使得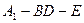 為直二面角.
為直二面角.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
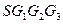 中,E、F分別是邊
中,E、F分別是邊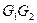 、
、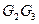 的中點,D是EF的中點,現(xiàn)沿SE、SF及EF把這個正方形折成一個幾何體(如圖乙所示),使
的中點,D是EF的中點,現(xiàn)沿SE、SF及EF把這個正方形折成一個幾何體(如圖乙所示),使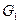 、
、 、
、 三點重合于點G,則下面結論成立的是( )
三點重合于點G,則下面結論成立的是( )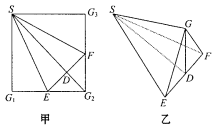
| A.SD⊥平面EFG | B.GF⊥平面SEF | C.SG⊥平面EFG | D.GD⊥平面SEF |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com